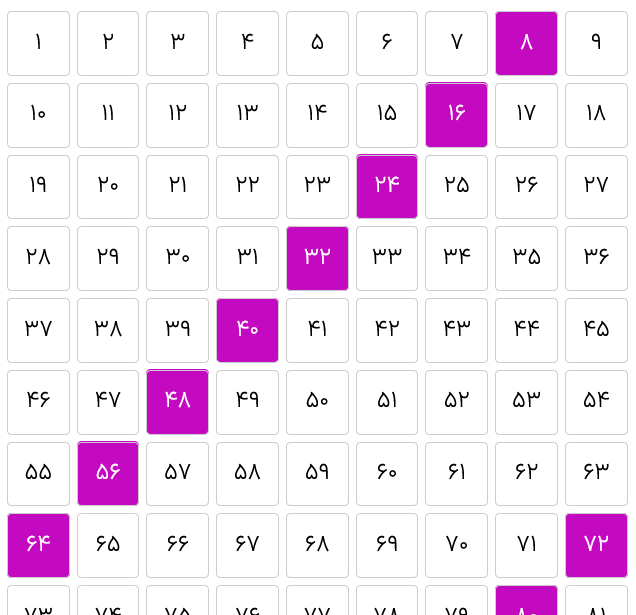
به جدول روبه‌رو نگاه کنید.
چطور توصیف می‌کنید که کدام خانه‌ها رنگی شده‌اند؟
اگر بتوانید جدول اعداد را طوری تغییر دهید که تعداد ستون‌ها، از ۲ ستون تا ۱۰ ستون تغییر کند، در هر جدول چندستونی، با رنگ کردن چه عددهایی می‌توانید الگویی مشابه با این الگوی رنگی، بسازید؟
شرح فعالیت
گام اول
این فعالیت نیازی به مقدمه‌چینی ندارد. با طرح مسئله آغاز کنید.
در ابزار مجازی «شمارش چندتا چندتا در جدول اعداد» ، جدول را در ۱۰ ستون بچینید و رنگ زدن ۹تا ۹تا را انتخاب کنید یا تصویر بالا را به نمایش بگذارید و از دانش‌آموزان بخواهید جدولی که می‌بینند و الگوی خانه‌های رنگی آن را توصیف کنند.
می‌توانید با پرسیدن چند سوال دانش آموزان را ترغیب کنید که به ادامه‌ی الگوی خانه‌های رنگی هم فکر کنند و توصیف خود را شفاف‌تر نمایند. مثلاً بپرسید:
- اگر جدول را ادامه دهیم، خانه‌ی بعدی که رنگ می‌شود چه عددی است؟
- عدد ۹۰ در ستون آخر رنگ شده است، اگر جدول را ادامه دهیم، آیا باز هم خانه‌ی از ستون آخر رنگ می‌شود؟ چه خانه یا خانه‌هایی؟ چطور استدلال می‌کنید؟
- چند تا عدد بزرگ بگویید که در صورت ادامه دادن جدول، رنگی می‌شوند. چطور این عددها را پیدا می‌کنید؟
گام دوم
در ادامه، جدول اعداد با ستون‌های متنوع را برای دانش‌آموزان توصیف کنید، مثلاً بگویید: «اعداد را به ترتیب سطر به سطر و از چپ به راست، در یک جدول چندستونی می‌چینیم.» در این مرحله نشان دادن همان ابزار مجازی «شمارش چندتا چندتا در جدول اعداد» بدون رنگ کردن خانه‌ها و تغییر دادن تعداد ستون‌ها در آن بسیار کارآمد است.
حالا از دانش‌آموزان بپرسید:
- در هر جدول چندستونی، اگر بخواهیم الگویی مشابه با الگوی رنگی قبلی بسازی، باید چه عددهایی را رنگ کنیم؟
به آن‌ها فرصت دهید که تنهایی فکر کنند و ایده‌هایشان را روی کاغذ بیاورند. برگه‌ی شطرنجی با خانه‌های ۱۰ میلی‌متر در ۱۰ میلی‌متری از ابزار کاغذی «برگه‌های شطرنجی» می‌تواند برای بازنمایی ایده‌ها به دانش‌آموزان کمک کند. همچنین می‌توانید ابزار مجازی «شمارش چندتا چندتا در جدول اعداد» را در یک دستگاه در کلاس داشته باشید که دانش‌آموزان بتوانند با هماهنگی با شما، درستی فرضیه‌هایی را که می‌سازند، با این ابزار بررسی کنند.
در ادامه، پس از آن که دانش‌آموزان فرصت کافی در اختیار داشتند، از آن‌ها بخواهید در گروه‌های دو تا چهار نفره قرار بگیرند و درباره‌ی ایده‌هایشان باهم گفت‌وگو کنند.
هنگامی که دانش‌آموزان مشغول کار گروهی هستند، به آن‌ها سر بزنید و با پرسیدن سوال‌هایی مانند سوال‌های زیر به آن‌ها کمک کنید که ایده‌های خود را شفاف کنند، برای آن‌ها دلیل بیاورند و ایده‌ها را تعمیم دهند. همچنین ایده‌های دوستانشان را بشنوند و ارزیابی کنند.
- آیا درک شما از صورت مسئله با هم یکسان بود؟
- آیا پاسخی که دوستتان پیدا کرده است با توجه به درکی که از صورت مسئله داشته است، درست است؟ چطور متوجه شدید؟
- چطور می‌توانیم همه‌ی حالت‌های مشابه در جدول‌های ۲ستونی تا ۱۰ستونی را پیدا کنیم؟
- در حالت کلی وقتی یک جدول با n ستون داریم، با رنگ کردن مضرب‌های چه عدد یا عددهایی می‌توانیم الگوی خانه‌های رنگی مورّب به پایین و چپ، بسازیم؟
- در حالت کلی وقتی یک جدول با n ستون داریم، با رنگ کردن مضرب‌های چه عدد یا عددهایی می‌توانیم الگوی خانه‌های رنگی مورّب به پایین و راست، بسازیم؟
در پایان از دانش‌آموزان بخواهید تا هر یک به تنهایی پاسخش را بنویسد و برای آن دلیل بیاورد.
پاسخ‌های برخی از دانش‌آموزان
مورّب به پایین و چپ، وقتی هست که خانه‌های مضربِ یکی کمتر از تعداد ستون‌ها (۱ – n) را رنگ کنیم.
چون هر بار یکی عقب می‌رویم.
مثلاً ۹تا ۹تا در جدول ۱۰ستونی.
مورّب به پایین و راست، وقتی هست که خانه‌های مضربِ یکی بیشتر از تعداد ستون‌ها (۱ + n) را رنگ کنیم.
چون هر بار یکی جلوتر می‌رویم.
مثلاً ۱۱تا ۱۱تا در جدول ۱۰ستونی.
بازخورد معلم: پاسخت از دو جنبه برایم جالب بود. یکی این که دو حالت مشابه را از هم جدا کرده‌ای و برای هر دو پاسخی نوشته‌ای و دیگر این که دلیل پاسخت را هم نوشته‌ای.
من فکر کردم که ۹تا ۹تا در جدول ۱۰ستونی را دیدیم.
۳تا ۳تا هم مشابه همان است. در ۳تا ۳تا، همان ۹تا ۹تا هم رنگ شده چون سه تا ۳تایی می‌شود ۹تا.
پس وقتی ۳تا ۳تا می‌شماریم، ۹تا ۹تا هم رنگ می‌شود.
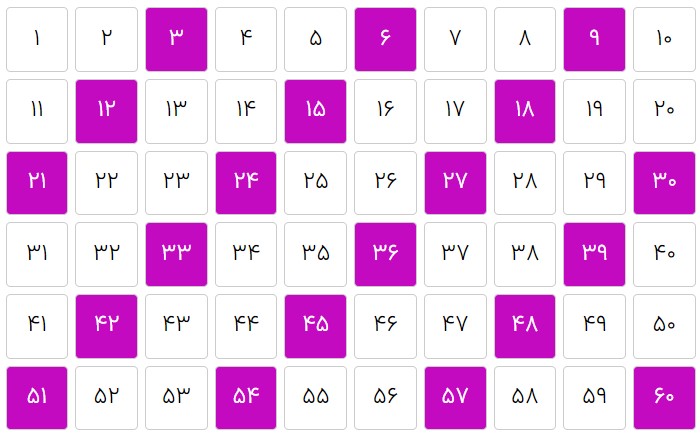
خب … من فکر کردم که اگر جدول ۹ستونی بود، چه می‌شد.
۸تا ۸تا که مورّب به عقب می‌شد چون وقتی یکی پایین می‌آیی ۹ تا جلو رفته‌ای و وقتی ۸ تا جلو بروی، یکی به پایین و یکی به عقب رفته‌ای.
بعد فکر کردم که ۴تا ۴تا و ۲تا ۲تا شمردن هم در جدول ۹ستونی مثل ۸تا ۸تا شمردن است. چون وقتی با اینها جلو می‌روی هم ۸تا ۸تا هم رنگ می‌شوند.
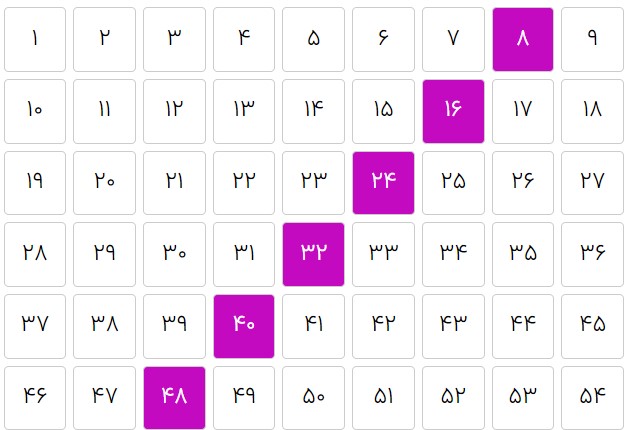
۸تا ۸تا
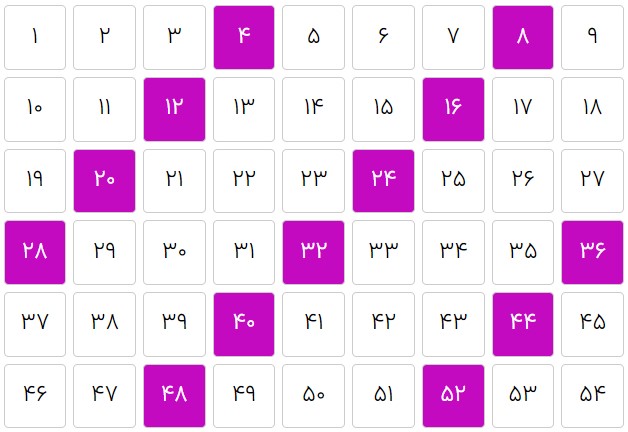
۴تا ۴تا
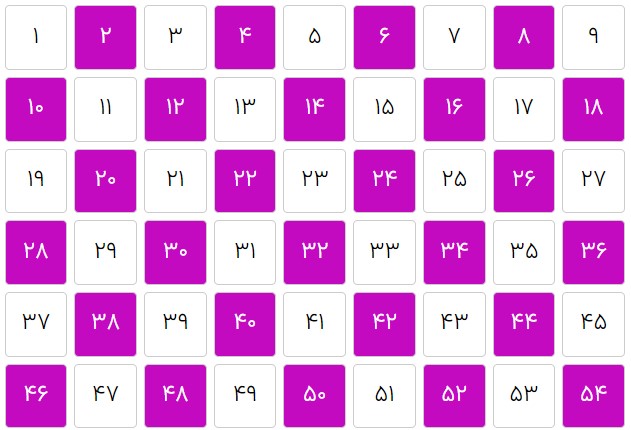
۲تا ۲تا
الگوی ۸تا ۸تا و ۴تا ۴تا شبیه هم است. هر دو مورب به چپ پایین هستند.
شاید به نظر برسد که شکل رنگ شدن ۲تا ۲تا با آن دو تا الگوی دیگر متفاوت است. اما به نظر من همان شکلی است، وقتی ۲تا ۲تا رنگ می‌کنیم، چند تا مورب به هم چسبیده داریم؛ مثلاً ۲ و ۱۰ را با هم ببینید، مورّب به پایین و چپ است، ۴ و ۱۲ و ۲۰ و ۲۸ هم همینطور و …
بازخورد معلم: چه خوب منظورت را نوشته‌ای. دلیل مورب بودن الگوی ۸تا ۸تا در جدول ۹ستونی را هم خوب توضیح داده‌ای.
آیا می‌توانی با توجه به تجربه‌ات در حل این مسئله، توضیح دهی که در جدول ۱۵ ستونی، با شمارش و رنگ کردن چندتا چندتا و کدام عددها الگویی مورّب دیده می‌شود؟
در جدول nستونی، مضرب‌های ۱- n و همه‌ی شمارنده‌های دیگرِ ۱ – n، شبیه الگوی نمایش داده شده است.
بازخورد معلم: ممنون که ایده‌ات را نوشتی. لطفا توضیح بده، یعنی بنویس که چه دلیلی برای ایده‌ات داری. راستی این که نوشتی «شمارنده‌های دیگرِ …» برایم جالب بود.
همین طرح یادگیری را می‌توانید با نشان دادن الگوهای دیگری از شمارش چندتا چندتا در جدول اعداد انجام دهید. مثلاً با جدولی که در آن مضرب‌های ۵ در جدول ۱۰ستونی رنگ شده‌اند.
توصیف این الگو و پیدا کردن الگوهای مشابه آن در جدول‌های چندستونی، ساده‌تر از فعالیت اصلی است.
دیدگاهتان را بنویسید