شمارش چندتا چندتا در جدول ۱ تا ۱۰۰

جدول ۱ تا ۱۰۰ را به هر یک از دانش‌آموزان (یا به گروه‌های دو نفره) بدهید. می‌توانید از ابزار کاغذی «جدول ۱ تا ۱۰۰» استفاده کنید.

از دانش‌آموزان بخواهید که با یک عدد خاص شروع کنند و با همان عدد چندتا چند تا بشمارند و خانه‌هایی را که می‌گویند، رنگ کنند؛ به عبارت دیگر مضرب‌های یک عدد را در جدول رنگ‌آمیزی کنند.

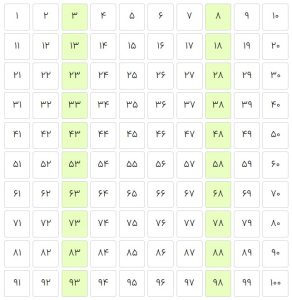
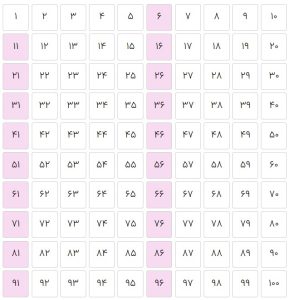
مثلاً ممکن است یکی از ۹ شروع کند و نه‌تا نه‌تا بشمارد و دیگری از ۵ شروع کند و پنج‌تا پنج‌تا بشمارد و جدول را مانند شکل‌های زیر رنگ کنند. 

سپس از بچه‌ها بخواهید که جدول‌های رنگ شده را روی دیوار کلاس بچسبانند، جدول‌های یکدیگر را ببینند و در یک گفت‌وگوی جمعی، درباره‌ی شباهت‌ها و تفاوت‌های این جدول‌ها صحبت کنند. نمونه‌هایی از آنچه ممکن است دانش‌آموزان در این گفت‌وگوی جمعی بگویند در انتهای این طرح یادگیری آمده است.

برای گفت‌و گو درباره‌ی جدول‌های رنگ شده، می‌توانید از ابزار مجازی «جدول ۱ تا ۱۰۰» استفاده و خانه‌های آن را هنگام گفت‌وگو و برای بازنمایی آنچه دانش‌آموزان می‌گویند، رنگ کنید.مثلا وقتی دانش‌آموزی درباره‌ی مضرب‌های ۹ صحبت می‌کند، خانه‌های مضرب ۹ را نشان دهید.

خوب است وقتی بچه‌ها الگویی را بیان می‌کنند، کلاس را دعوت کنید که استدلالی برای درست بودن آن بیاورند. مثلا می‌توانید سوال‌های زیر را بپرسید:

• چرا در شمارش نه‌تا نه‌تا خانه‌ی رنگی در هر ردیف به عقب می‌رود؟
• آیا اگر عددها را ادامه دهیم و ردیف‌های بیشتری داشته باشیم، بازهم الگوی خانه‌های رنگی به همین ترتیب ادامه پیدا می‌کند؟ چرا؟