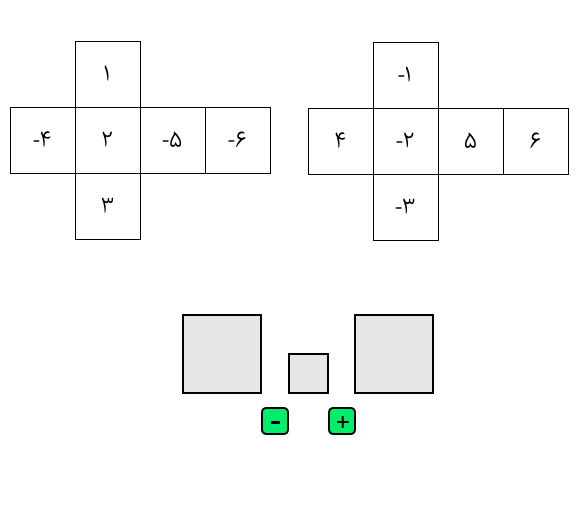
این جدول، صفحهی بازی دوز اعداد صحیح است.
برای این بازی دو تا تاس نیاز دارید که روی یکی اعداد ۱ و ۲ و ۳ و ۴- و ۵- و ۶- و روی دیگری اعداد ۱- و ۲- و ۳- و ۴ و ۵ و ۶ نوشته شده باشد. به نوبت بازی کنید و هر دو تا تاس را بیندازید. عددهای روی تاس را به ترتیب دلخواه در یک عبارت جمع یا تفریق قرار دهید و حاصل را به رنگ خودتان رنگ کنید.
برندهی بازی کسی است که زودتر از دیگری ، سه خانهی کنار هم افقی، عمودی یا مورب را به رنگ خود درآورد.

شرح فعالیت
از دانشآموزان بخواهید در گروههای دو نفره قرار بگیرند. کاربرگ «دوز اعداد صحیح» را در اختیارشان قرار دهید و از آنها بخواهید شرح بازی را بخوانند و با گفتوگو باهم مطمئن شوند که بازی را درست متوجه شدهاند.
وسایل لازم برای بازی یعنی دو رنگ مداد و دو تا تاس عددهای صحیح را هم در اختیار گروه ها بگذارید. برای ساختن تاس ها میتوانید با گداشتن علامتی کنار برخی عددهای تاس معمولی، تاسهای لازم را بسازید.
وقتی دانشآموزان مشغول بازی شدند به گروهها سر بزنید و مطمئن شوید که بازی را درست انجام میدهند.
بعد از یک دور بازی، ابزار کاغذی «صفحهی بازی دوز اعداد صحیح» را در اختیار دانشآموزان قرار دهید (میتوانید این صفحههای بازی را پشت همان کاربرگ قبلی چاپ کنید).
در ادامه باز هم به گروهها سر بزنید و ببینید چطور تصمیم میگیرند که هر کدام از عددهای روی تاس را در کدام جای خالی قرار دهند و کدام علامت را بین آنها قرار دهند.
با پرسیدن سوالی مانند سوال زیر، توجه آنها را به فرصتهایی که برای انتخاب دارند، جلب کنید:
- در هر دور بازی وقتی تاس میاندازی، میتوانی انتخاب کنی که دو عدد را به چه ترتیبی قرار دهی و میتوانی انتخاب کنی که بین آنها علامت جمع بگذاری یا تفریق. یعنی حالتهای مختلفی داری و میخواهی بهترین انتخاب را انجام دهی. برای این که همهی حالتها را بررسی کنی، چند تا جمع یا تفریق باید انجام بدهی؟
دانشآموزان ممکن است پاسخهای مختلفی برای این پرسش ارائه کنند، حتی ممکن است پاسخ اولیهای بدهند، اما در ادامه و وقتی هنگام بازی، بیشتر به انتخابهایشان فکر میکنند، پاسخهایشان تغییر کند.
نمونههایی از پاسخهای دانشآموزان
چهار حالت
عددها را میگذارم و یک جمع و یک منها انجام میدهم. بعد عددها را جابهجا میکنم و دوباره یک جمع و یک منها انجام میدهم، یعنی چهار تا عبارت را محاسبه میکنم تا بهترین آنها را برای خودم انتخاب کنم.
سه حالت
علامت جمع را میگذارم. در این حالت فرقی ندارد که کدام عدد کدام طرف باشد، چون در جمع فرقی نمیکند که عدد بزرگ تر اول باشد یا عدد کوچکتر. من فکر نمیکردم دربارهی عددهای منفی هم این کار را بتوان کرد ولی انجام دادم و دیدم که فرقی نمیکند.
حالا علامت تفریق را میگذارم. اینجا فرق میکند که کدام عدد کدام طرف باشد و برای همین هر دو حالت را امتحان میکنم.
دو حالت!
جمع ویژگی جابهجایی دارد. پس یک حالت این است که دو عدد را باهم جمع کنم و با جابهجا کردن عددها فرقی در حاصل ایجاد نمیشود.
تفریق ویژگی جابهجایی ندارد؛ ولی وقتی اولین عدد را منهای دومی میکنم و بعد جای عددها را جابهجا میکنم، حاصل قرینه میشود.
مثلاً ۳=۲-۵ و ۳-=۵-۲
من امتحان کردم، در همهی عددهای من اینطوری شد.
دو حالت
a+b=b+a
a-b=a+(-b)=-(-a)+(-b)=-(-a+b)=-(b-a)
این یعنی:
یک بار دو عدد را جمع میکنم که فرقی ندارد با چه ترتیبی.
یک بار ترتیبی را برای تفریق مینویسم که برایم راحتتر است و بعد، خود عدد حاصل و قرینهی آن را پیدا میکنم.
پس سه تا عدد دارم که باید ببینم کدام برایم بهتر است.
به دانشآموزان سر بزنید و دلایل آنها را بشنوید، حواستان باشد که نیازی نیست که همهی بچهها مثل هم فکر کنند. در نوشتهای به نام گوناگونسازی- بازیهای لایهدار دربارهی لایههای این فعالیت و مزیت این لایهدار بودن صحبت شده است.
دیدگاهتان را بنویسید