گوناگون‌سازی (۱)

وقتی از استفاده از بازی در کلاس درس حرف می‌زنیم، معمولاً به جذاب شدن کلاس فکر می‌کنیم و این که همین جذابیت می‌تواند نقطه‌ی وصل بعضی از دانش‌آموزان به کلاس و حتی به ریاضی باشد. وقتی می‌خواهیم بازی انتخاب کنیم، بعضی بازی‌ها به نظرمان بازی‌های جذاب‌تری هستند، اما بعضی بازی‌ها، بازی‌های بهتری هستند و غیر از جذابیت، چیزهای دیگری هم دارند. سوال این است که با چه معیاری می‌گوییم: «یک بازی بهتر از بازی دیگر است؟»

در این نوشته می‌خواهم به بازی‌هایی اشاره کنم که از یک منظر بازی‌های بهتری هستند. من اسمشان را گذاشته‌ام بازی‌های لایه‌دار، یعنی بازی‌هایی که مستقل از لایه‌ی رویی، لایه‌های دیگری هم دارند و بچه‌ها با توجه به سطح شناختشان ممکن است وارد لایه‌های عمیق‌تر بازی شوند.

بگذارید با یک مثال موضوع را شفاف‌تر کنم. به بازی «دوز اعداد صحیح» توجه کنید، چند لحظه‌ای خواندن را رها کنید و بازی را انجام دهید:

در این بازی به نوبت انجام می‌شود و هر بازیکن باید در نوبت خود، دو تا عدد برآمده از تاس‌های زیر را در جاهای خالی قرار دهد و انتخاب کند که می‌خواهد بین آن‌ها علامت جمع بگذارد یا تفریق.

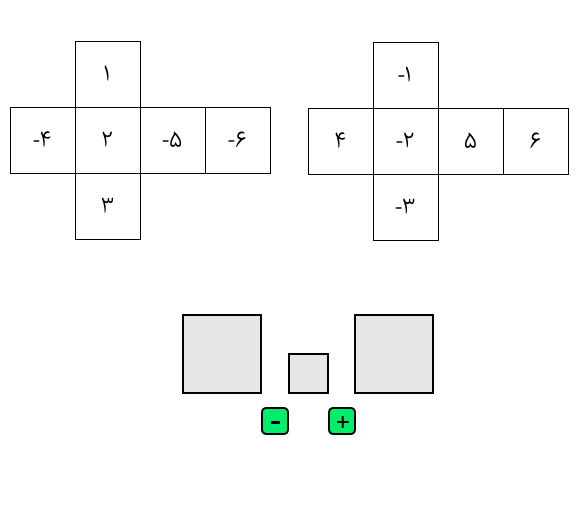
در ادامه او باید حاصل به دست آمده را در صفحه‌ی بازی به رنگ خودش درآورد و برنده کسی است که زودتر از دیگری، سه خانه‌ی افقی، عمودی یا مورب کنار هم را رنگ کند.

این بازی می‌تواند جایگزین برخی تمرین‌های جمع و تفریق اعداد صحیح شود؛ چرا که در آن ضمن آن که بچه‌ها جمع و تفریق می کنند، درستی جمع و تفریق هم‌بازیشان را هم بررسی می‌کنند و در یک مدت کوتاه تعداد زیادی جمع و تفریق انجام می‌دهند. این لایه‌ی اول این بازی است.

اما با یک سوال کوچک می‌توان بچه‌ها را به سمت کشف لایه‌های دیگر برد. سوال این است: «در هر دور بازی وقتی تاس می‌اندازی، می‌توانی انتخاب کنی که دو عدد را به چه ترتیبی قرار دهی و می‌توانی انتخاب کنی که بین آن‌ها علامت جمع بگذاری یا تفریق. یعنی حالت‌های مختلفی داری و می‌خواهی بهترین انتخاب را انجام دهی. برای این که همه‌ی حالت‌ها را بررسی کنی، چند تا جمع یا تفریق باید انجام بدهی؟»

من این سوال را از بچه‌های زیادی هنگامی که دوتا دوتا مشغول بازی بوده‌اند، پرسیده‌ام. اولین پاسخ در اکثر موارد چهارتا بوده است، دو تا جمع و دو تا تفریق و معمولاً هر دو بازیکن با این پاسخ از همان ابتدا موافق بوده‌اند یا به سرعت توانسته‌اند همدیگر را قانع کنند. اما دقایقی بعد اتفاق‌های دیگری می‌افتد. معمولاً بعد از این سوال، بچه‌ها با دقت بیشتری به جمع و تفریق‌هایی که انجام می‌دهند، نگاه می‌کنند. در دور بعدی که به سراغشان می‌روم در بیشتر گروه‌ها درباره‌ی جابه‌جایی جمع حرف می‌زنند و می‌گویند که می‌توان یکی از چهار حالت‌ را بررسی نکرد، چون در جمع می‌توان عددها را جابه‌جا کرد.

یکی از مزایای انجام این بازی به جای تمرین، شناختی است که من به عنوان معلم هنگام شنیدن پاسخ‌ها به‌دست می‌آورم. مثلاً وقتی یکی از بچه‌ها درباره‌ی جابه‌جا شدن عوامل جمع حرف می‌زند و دیگری با شگفتی او را نگاه می‌کند و باور نمی‌کند که جابه‌جا شدن عوامل در همه‌ی جمع‌ها اثری در حاصل ندارد، یکی از فرصت‌های شناخت است، استدلال‌هایی که دیگری برای تعمیم خاصیت جابه‌جایی می‌آورد نیز فرصت دیگری است.

اما هنوز لایه‌های این بازی تمام نشده‌است. معمولاً چند نفری در کلاس هستند که ایده‌ی دیگری هم دارند. آن‌ها می‌گویند که می‌توان یکی از تفریق‌ها را هم انجام نداد و پاسخش را با قرینه کردن پاسخ تفریق دیگر، پیدا کرد. دست و پا زدن این بچه‌ها برای بیان ایده و استدلال برای درستی آن دیدنی و شنیدنی است.

آنچه من می‌خواهم به آن به عنوان لایه‌ای از این بازی اشاره کنم، فرصت طرح فرضیه است که در فعالیت‌های معمولی بچه‌ها انگیزه‌ای برای آن ندارند. این که بچه‌ها خودشان فرضیه‌ای می‌سازند و برای استدلال درباره‌ی آن تلاش می‌کنند، لایه عمیقی است که البته برای برخی از بچه‌ها شدنی و در دسترس است.

امیدوارم منظورم از فعالیت لایه‌دار با این مثال و توضیحاتی که در ادامه‌ی آن آمد، روشن شده باشد.

آن‌چه باعث می‌شود لایه‌دار بودن یک بازی یا فعالیت، مزیتی برای آن به حساب آید، فرصتی است که برای گوناگون‌سازی^۱ آموزش ایجاد می‌کند.

لطفاً به عبارت «فرصتی است که برای گوناگون‌سازی آموزش ایجاد می‌کند» با دقت بیشتری نگاه کنید. معلم انتخاب نمی‌کند که به هر کدام از بچه‌ها در چه سطحی مسئله بدهد، حتی خود بچه‌ها هم با توجه به پیشینه و توانایی‌هایی که دارد، سطح مسئله‌‌‌ی مورد نظرشان را انتخاب نمی‌کنند؛ این انتخاب طبیعی رخ می‌دهد و خود بازی است که این فرصت را ایجاد می‌کند. همه مشغول انجام یک بازی هستند. هیچ‌کس احساس ناتوانی ندارد، مثل یک تمرین ساده، ممکن است برخی سریع‌تر و برخی کندتر باشند، اما برخلاف یک تمرین ساده، بچه‌ها در سطح‌های مختلفی مشغول حل مسئله هستند. در مثال بالا، بعضی از بچه‌ها مشغول حساب کردن هستند، برخی از حساب جمع و تفریق اعداد صحیح، وارد جبر و برخی وارد استدلال‌های جبری می‌شوند.

این که همه‌ی بچه‌ها روی یک بازی کار می‌کنند و تکلیف‌های متنوع ندارند اما در سطح‌های گوناگون و متناسب با شناختشان مسئله حل می‌کنند، جالب است. این شکل از گوناگون‌سازی آموزش اثر مخرب جداسازی بچه‌ها و حس تمایز را در بچه‌ها کم‌رنگ می‌کند. جالب‌تر از آن این است که چون بازی شانسی است، بچه‌هایی که در سطح بالاتر کار می‌کنند، تبدیل به همیشه برنده نمی‌شوند و هیجان بازی برای بچه‌هایی که در سطح پایین‌تر مشغول جمع و تفریق هستند، همچنان باقی می‌ماند.

پی‌نوشت:

این بازی را چند باری با دانش‌آموزان خودم تجربه کرده‌ام؛ اما آخرین باری که بازی را دیدم، سال ۱۳۹۸ بود که مهمان کلاس محدثه کشاورز و راضیه جلالی بودم. ممنونم که مرا در کلاسشان مهمان کردند.

1. Differentiation ↩︎