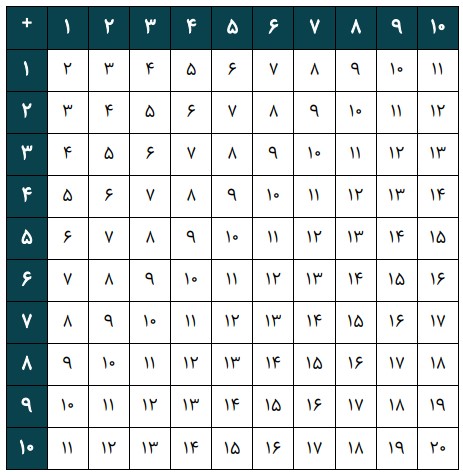
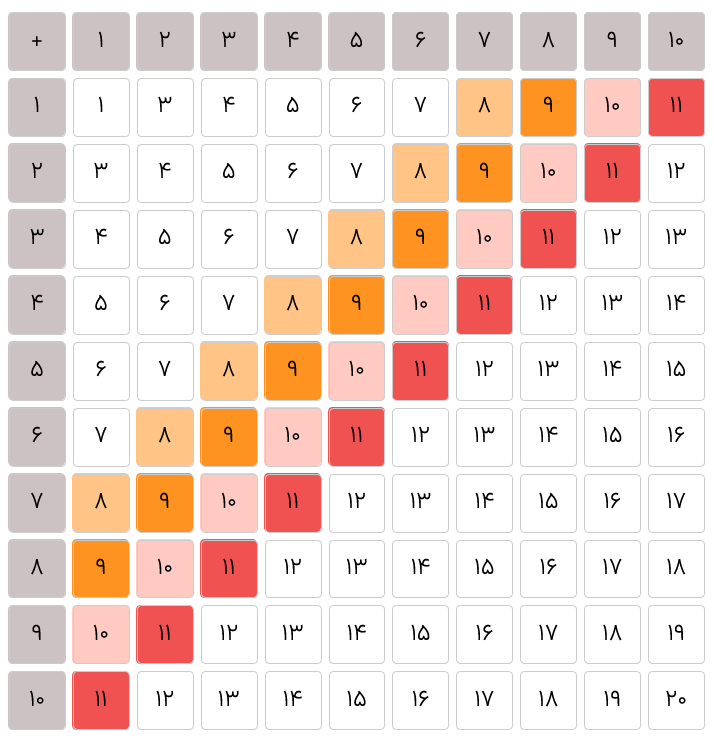
یک مستطیل دلخواه با ضلعهای افقی و عمودی، روی جدول جمع رسم کردهایم، طوری که هر رأس آن روی یکی از عددهای جدول باشد.
در این مستطیل حاصل جمع عددهای روی رأسهای دو قطر باهم برابر است؛ یعنی ۱۳+۹=۱۶+۶.
شما هم مستطیلهای دیگری رسم کنید.
آیا همیشه حاصل جمع عددهای روی رأسهای دو قطر باهم برابرند؟ چرا؟

شرح فعالیت
جدول جمع را در اختیار دانشآموزان قرار دهید و از آنها بخواهید یک مستطیل دلخواه با ضلعهای افقی و عمودی روی آن رسم کنند و عددهای روی رأسهای هریک از قطرهای مستطیل را با هم جمع کنند. از آنها بپرسید: «آیا دو عدد با هم مساوی شد؟» (اگر درست محاسبه کرده باشند، باید دو عدد مساوی شده باشند).
برای این فعالیت میتوانید از ابزار کاغذی «جدول جمع» یا ابزار مجازی «جدول جمع» استفاده کنید و روی آنها صورت مسئله را توضیح دهید یا به جای آنها اولین فایل کاربرگ «چهارضلعیها روی جدول جمع» را در اختیار دانشآموزان قرار دهید.
در ادامه این ادعا را مطرح کنید:
«وقتی مستطیلی با ضلعهای افقی و عمودی روی جدول جمع رسم میکنیم، حاصل جمع عددهای روی رأسهای دو قطر با هم برابر است!»
از دانشآموزان بخواهید در گروههای کوچک (دو تا چهار نفره) قرار بگیرند و درستی یا نادرستی این ادعا را در حالت کلی ثابت کنند.
برای آنها توضیح دهید که حتی اگر بتوانند یک مثال در همین جدول جمع یا در ادامهی آن، یعنی وقتی جدول را از راست و پایین ادامه میدهیم، پیدا کنند، کار تمام است و ثابت شده که این ادعا در حالت کلی درست نیست.
اما برای اثبات این که این ادعا درست است، باید نشان دهند که با جابهجا شدن و بزرگ و کوچک شدن مستطیل، باز هم این ادعا درست است.
وقتی گروهها مشغول کار هستند به آنها سر بزنید و با پرسیدن سوالهای مناسب، به آنها کمک کنید تا بتوانند ایدههایشان را شفافتر بگویند و ایدههای یکدیگر را ارزیابی کنند. مثلاً بپرسید:
- منظورت این است که «هر دو عدد سمت چپ به یک اندازه از دو عدد سمت راست بیشترند»؟
- آیا این ایده دربارهی مستطیلهای دیگر هم درست است؟
- آیا با دوستت موافقی؟
- آیا میتوانی همین را که گفتی، با استفاده از یک یا چند عبارت جبری بنویسی؟
اهمیت استدلال
لابلای حرفهای بچهها به دنبال استدلال بگردید.
دانشآموزان ممکن است برای ایدههایشان دلیل بیاورند، اما خودشان متوجه نباشند که این دلیل، یک دلیل کلی است یا میتواند منجر به استدلالی کلی دربارهی همهی حالتها شود. به آنها کمک کنید که ایدههایشان را تعمیم دهند و در حالت کلی بیان کنند.
زمانی که گروهها به اندازهی کافی فرصت برای فکر کردن و ایدهپردازی و جمعبندی داشتند، از آنها بخواهید ایدههایشان را در کلاس مطرح کنند و ایدههای یکدیگر را مورد ارزیابی قرار دهند.
برای آنکه ایدههای جدید در کلاس طرح شود، با یک گروه آغاز کنید و سپس از گروههای دیگر بپرسید که آیا راهحل مشابه یا متفاوتی برای مطرح کردن، دارند؟
در این مرحله میتوانید از ابزار مجازی «جدول جمع» برای نشان دادن مثالهای گروههای مختلف در کلاس استفاده کنید.
در پایان از دانشآموزان بخواهید هر یک به تنهایی، دلیلی را که به نظرش قابل دفاع است، به هر ترتیبی که میخواهد، بنویسد.
پاسخهای برخی از دانشآموزان
من دیدم که دو تا عدد سمت راست به یک اندازه بیشتر از عددهای سمت چپ هستند. برای همین دو عدد سمت راست را همان عددهای سمت چپ بهعلاوهی a در نظر گرفتم و همانطور که اینجا نوشتهام، جمع عددهای دو قطر با هم مساوی شد:
x+(y+a)=y+(x+a)
x+y+a=x+y+a

بازخورد معلم: ایدهات را خیلی خوب نوشتهای و به زبان ریاضی در آوردهای.
آیا مطمئنی که همیشه دو عدد سمت راست به یک اندازه بیشتر از عددهای سمت چپ هستند؟ آیا میتوانی برای آن دلیل بیاوری؟
من یک مستطیل در حالت کلی کشیدم و نوشتم که خانهها چطور از مجموع دو عدد ساخته میشوند.
حاصل جمع عددهای روی رأسهای هر قطر برابرست با:
(b+d)+(a+c)=(b+c)+(a+d)
a+b+c+d =



دیدگاهتان را بنویسید