عقربهی هر دو چرخنده را میچرخانیم و عددهایی را که عقربهها نشان میدهند، باهم جمع میکنیم.
هرکس که حاصل را روی کارتش داشته باشد، میتواند آن را خط بزند. برنده کسی است که همهی عددهای کارتش، زودتر از بقیه خط بخورد.
نُه عدد مختلف روی کارتت بنویس و کارت بازی خودت را بساز!
چطور میتوانی یک کارت بازی بسازی که بیشترین شانس بردن را داشته باشد.
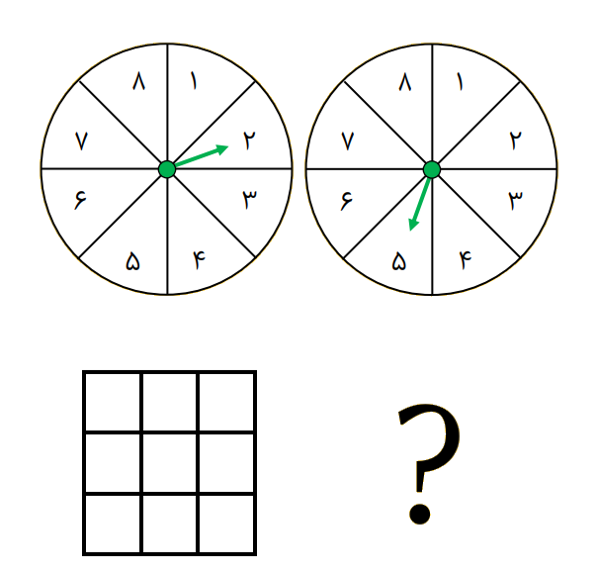
شرح فعالیت
گام اول؛ دستور بازی
شرح بازی با دو چرخنده را به دانشآموزان نشان دهید و فرصت دهید تا شرح بازی را بخوانند. برای این منظور میتوانید از اولین فایل پوستر «بازی با دو چرخنده» استفاده کنید.
با پرسیدن سوالات زیر، مطمئن شوید که شرح بازی را فهمیدهاند.
- بازی چه زمانی تمام میشود؟
- در چرخندههایی که در تصویر دیده میشود، چه عددی خط میخورد؟
گام دوم؛ انجام بازی
در ادامه از دانشآموزان بخواهید جدولی رسم کنند، به صورت فردی فکر کنند و عددهای مورد نظر خود را در آن بنویسند.
پس از آنکه دانشآموزان عددهای جدول خود را کامل کردند، میتوانید بازی کنید و فرصتی فراهم کنید که دانشآموزان کمی بیشتر با بازی آشنا شوند و با پرسیدن سوالهایی مانند سوالهای زیر، مطمئن شوید که همهی آنها میدانند که حاصل شدن اعداد کوچکتر از ۲ و بیشتر از ۱۶، غیر ممکن است.
- چه عددهایی ممکن است از جمع کردن دو عدد روی چرخنده حاصل شود؟
- کدام عددها ممکن نیست به دست بیاید؟
گام سوم؛ حل مسئله
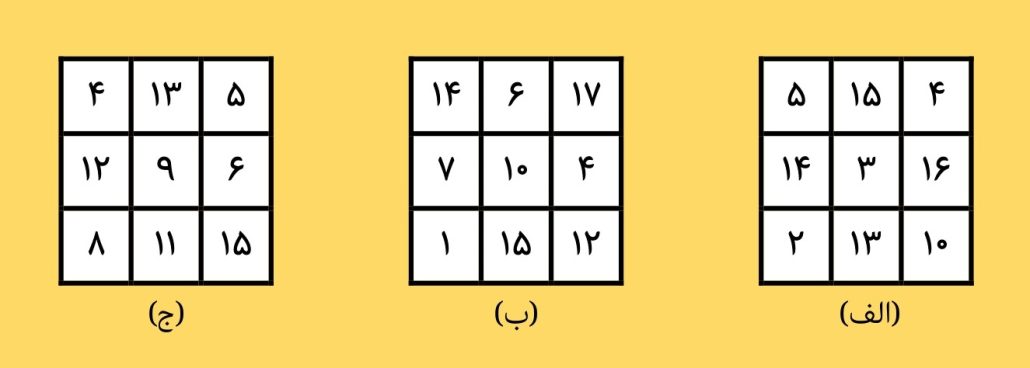
حالا از دانشآموزان بخواهید جدولهای (الف)، (ب) و (ج) را باهم مقایسه کنند و بررسی کنند که کدامیک انتخاب بهتری برای اعداد جدول است و بر اساس ایدههای خود، یک کارت بازی طراحی کنند که به نظرشان، بیشترین شانس بردن را دارد. دومین فایل پوستر «بازی با دو چرخنده» این مسئله را نشان داده است.
بعد از آن که دانشآموزان فرصت کافی برای فکر کردن داشتند، از آنها بخواهید در گروههای کوچک (دو یا سه نفره) قرار بگیرند و ایدههایشان را با هم به اشتراک بگذارند.
اهمیت استدلال
لابلای حرفهای بچهها به دنبال استدلال بگردید.
هنگامی که دانشآموزان مشغول گفتوگو هستند، به آنها سر بزنید و دلایل انتخابشان را بشنوید. گاهی ممکن است دلایل خوبی در کلاس مطرح شود. در صورت لزوم با بازگویی آن دلایل به صورت شفافتر، به دانشآموزی که این دلیل را ارائه کرده است، فرصت میدهید که روی بیان دلایل بازاندیشی کند و به دانشآموزان دیگر گروه کمک میکنید که دلیل را درک کنند و فرصت بهکارگیری آن در موقعیتهای دیگر را پیدا کنند.
در پایان از دانشآموزان بخواهید جدول نهایی را به تنهایی پر کنند و دلایل خود برای انتخاب اعداد را بنویسند.
پاسخهای برخی از دانشآموزان
جدول (ب) عددهای ۱ و ۱۷ را دارد و ممکن نیست برنده شود. جدول (ج) عددهایی مثل ۸ دارد که به نظر میرسد جمعهای بیشتری دارد ولی جدول (الف) عددی مثل ۲ را دارد که شانس آمدنش کم است و فقط وقتی حاصل میشود که هر دو چرخنده ۱ بیاید. من (ج) را انتخاب میکنم.
خودم هم این جدول را کشیدهام:

بازخورد معلم: پاسخهایت نشان میدهد که برای آنها دلیل داشتهای و تا حدودی استدلالهایت را نوشتهای.
لطفا توضیح بده:
- چرا نوشتهای «۸ جمعهای بیشتری دارد»؟
- چطور میتوانی همهی حالتهای ممکن را ثبت کنی؟
- چطور ثبت این حالتها کمک میکند که تشخیص دهی کدام کارت شانس بیشتری برای بردن دارد؟
جدول (ب) ممکن نیست برنده شود. جدول (الف) عددهایی نزدیک به هم دارد مثل ۱۳، ۱۴، ۱۵ و ۱۶ که به نظر میرسد شانسشان کم است ولی جدول (ج) عددهای پراکندهای دارد و شانسش زیاد است.
خودم هم این جدول را کشیدهام:

بازخورد معلم (با توجه به این که به نظر میرسد دانشآموز به اشتباه فکر میکند اعداد نزدیک به هم شانس کمتری دارند):
به درستی تشخیص دادهای که جدول (ب) ممکن نیست برنده شود ولی توضیحی برای آن ننوشتهای. جدول خوبی هم طراحی کردهای.
لطفا توضیح بده:
- چه عددهایی ممکن است از جمع عددهای روی دو چرخنده حاصل شود؟
- کدام عددهای جدول ممکن نیست که حاصل شوند؟
- چرا فکر میکنی که عددهای نزدیک به هم شانس کمتری دارند؟
- هر کدام از این عددهای ممکن در چه حالتهایی به دست میآیند؟
- چطور میتوانی از این حالتها برای یافتن احتمال حاصل شدن هر عدد استفاده کنی؟

جدول (ج) شانس بیشتری دارد چون در مجموع، حالتهای حاصل شدن عددهایش بیشتر است.
و خودم در جدولم اعداد ۶ و ۷ و ۸ و ۹ و ۱۰ و ۱۱ و ۱۲ و دو تا از عددهای ۴ یا ۵ یا ۱۳ یا ۱۴ را میگذارم.
بازخورد معلم (با توجه به این که دانشآموز حالتهای ۱+۲ و ۲+۱ را به اشتباه یکسان در نظر گرفته است): خیلی خوب ایدهات را صورتبندی کرده و توضیح دادهای.
لطفا به این سوالها فکر کن و پاسخت را کامل کن:
- در صورتی که چرخندهی سمت راست و سمت چپ چه عددهایی را نشان دهند، حاصل ۳ را خواهیم داشت؟
- چطور پاسخت به سوال قبل میتواند روی کل تعداد حالتهایی که برای هر عدد پیدا کردهای اثر بگذارد؟
- احتمال حاصل شدن هر یک از عددهای ۲ تا ۱۶ چقدر است؟
نکته: این دانشآموز به غیر ممکن بودن برنده شدن جدول (الف) اشاره نکرده است ولی صورت سوال آن را نخواسته است و به همین دلیل در بازخورد به آن اشاره نشده است.
من همهی حالتها را در جدول روبهرو مرتب کردم.
از روی این جدول فهمیدم که ۶۴ حالت ممکن است بهوجود بیاید که با هم همشتنس هستند.
احتمال هر کدام از حاصلهای ۲ تا ۱۶ را از روی این جدول پیدا کردم و از روی آنها احتمال هر کدام از عددهای جدول (الف) و (ج) را نوشتم و دیدم که جدول (ج) احتمال خط خوردن عددهایش بیشتر است. جدول (ب) هم غیر ممکن است ببرد؛ چون عدد ۱ را دارد که ممکن نیست حاصل شود.


اگر بخواهم خودم جدولم را بسازم، از عددهای ۵ تا ۱۳ استفاده میکنم که بین این اعداد بیشترین شانس خط خوردن را دارند.
بازخورد معلم: ایدهات برای حل این مسئله خیلی خوب بود و آن را خیلی خوب توضیح دادهای.
دیدگاهتان را بنویسید