میخواهیم ۳۶ بیسکویت را به طور مساوی بین تعدادی کودک تقسیم کنیم.
- به نظر شما به چند نفر، بیسکویت میرسد؟ به هر نفر، چندتا میرسد؟

شرح فعالیت
گام اول؛ مواجهه
۳۶ کاشی مربع شکل یا ۳۶ بیسکوییت به دانشآموزان نشان بدهید. به بچهها بگویید هر کدام از کاشیها نشاندهندهی یک بیسکویت هستند. ما میخواهیم این بیسکویتها را به طور مساوی بین تعدادی کودک تقسیم کنیم. کار امروز آنها این است که با همگروهی خود پیدا کنند که به چند کودک بیسکوییت میرسد و به هر کدام چندتا میرسد. به این موضوع اشاره کنید که پاسخهای زیادی برای این فعالیت وجود دارد و آنها باید تلاش کنند مسئله را با هر چند روش مختلفی که میتوانند حل کنند و همهی ایدههای خود را در دفترشان یا بر روی یک کاغذ نشان دهند.
گام دوم؛ کاوش
سپس به هر یک از گروهها ظرفی با ۳۶ کاشی مربعی (یا بیسکویت) بدهید. دانشآموزان به صورت دو نفره برای پاسخ به دو سوال کار خواهند کرد:
• بین چند کودک میتوان بیسکویتها را به طور مساوی تقسیم کرد؟
• به هر کودک چندتا بیسکویت میرسد؟
از گروهها بخواهید راهی برای ثبت هر یک از راهحلهای خود بیابند به طوری که هم از شکل و هم از عددها استفاده کنند. دانشآموزان را تشویق کنید تا تلاشهایی که به نظرشان موفقیتآمیز نبوده را هم ثبت کنند و در ثبتهایشان نشان دهند که چرا چیزی که امتحان کردند باعث ایجاد گروههای مساوی نشد.
گام سوم؛ گفتوگو
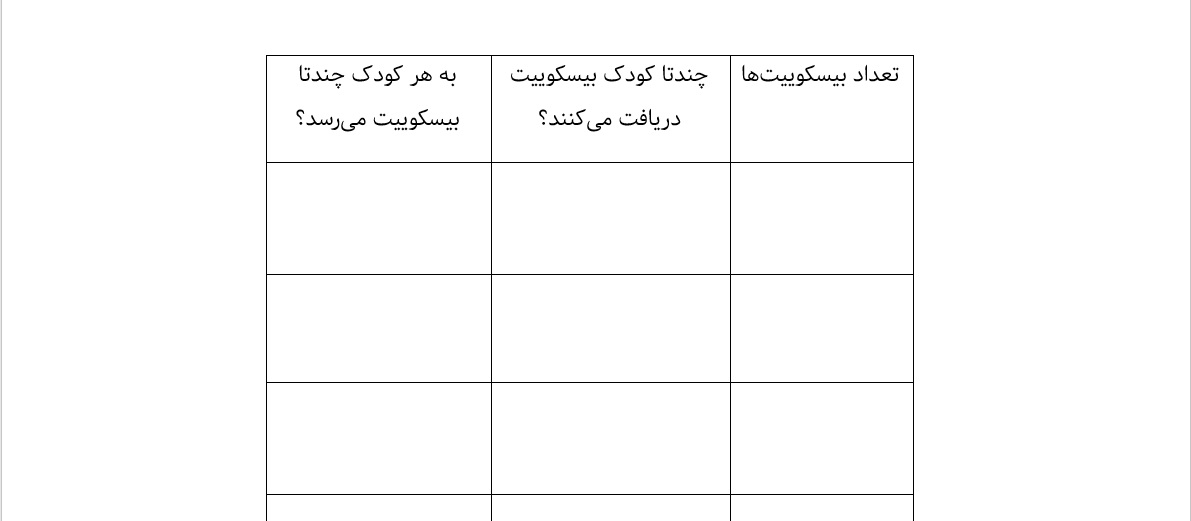
در مورد راهحلهایی که دانشآموزان پیدا کردند، گفتوگو کنید. راهحلها را در جدولی مانند شکل زیر با ستونهایی با عنوانهای «تعداد بیسکوییتها»، «چندتا کودک بیسکوییت دریافت میکنند؟» و «به هر کودک چندتا بیسکوییت میرسد؟»، سازماندهی کنید. به کاربرگ «سازماندهی تقسیم شراکتی بیسکوییتها» رجوع شود.

در یک جدول دیگر راهبردهایی که دانشآموزان استفاده کردند را ثبت کنید، مانند توزیع کردن کاشیها، استفاده از آنچه در مورد اعداد میدانند و دو برابر کردن و نصف کردن.
وقتی که تمام راهحلهای دانشآموزان را جمعآوری کردید، از دانشآموزان بپرسید:
- آیا ما همهی روشهایی را که میشد ۳۶ بیسکوییت را تقسیم کرد، پیدا کردیم؟ چرا بله یا چرا نه؟
گام چهارم؛ کاوش
دانشآموزان قرار است سوالات زیر را مورد کاوش قرار دهند:
- در راهحلهایی که پیدا کردیم، متوجه چه الگوهایی شدید؟
- چطور میتوانیم آنچه را که پیدا کردیم را سازماندهی کنیم تا بتوانیم الگوها را ببینیم؟
گروهها جدول را به عنوان کمکی برای دیدن الگوها در نظر میگیرند. به هر یک از گروهها کاربرگ «سازماندهی تقسیم شراکتی بیسکوییتها» را بدهید. البته بعضی از گروهها شاید روشهای دیگری را برای سازماندهی راهحلها برای دیدن الگوها ترجیح دهند.
اگر هنگام سازماندهی جدول و جستجو در مورد الگوها، دانشآموزان راهحلهای جدیدی را پیدا کردند، آنها را تشویق کنید تا آن راهحلهای جدید را در جدول کلاس اضافه کنند تا برای همهی دانشآموزان مورد استفاده و کاوش باشد.
گام پنجم؛ گفتوگو
کلاس را دور هم جمع کنید و در مورد سوالات زیر گفتوگو کنید:
- متوجه چه الگوهایی شدید؟
- چگونه آنچه را که پیدا کردید، سازماندهی کردید؟
- آیا ما همهی راهحلها را پیدا کردهایم؟ از کجا مطمئن هستید؟
همانطور که در مورد الگوهایی که دانشآموزان متوجه شدهاند صحبت میکنید، حتماً از آنها دعوت کنید تا در صورت امکان روشهایی را که جداول خود را سازماندهی کردهاند را به اشتراک بگذارند. وقتی دانشآموزان درباره الگوهایی که متوجه میشوند و استراتژیهایی که استفاده کردهاند بحث میکنند، از این فرصت استفاده کرده و برای دانشآموزان توضیح دهید که کاری که در تقسیم کردن یک گروه بزرگ به گروههای هم اندازه کوچکتر انجام میدهند، تقسیم کردن است. برخی از دانشآموزان از ضرب استفاده میکنند تا به کمک ساختن گروههای مساوی به تعداد کل برسند. اگر خود دانشآموزان هنوز واژگان لازم برای توصیف این مفاهیم را ندارند، این بهترین لحظه برای شماست تا به طور واضحی کلمات دقیق ریاضی را جایگزین آنها کنید. اگر هم ضرب و هم تقسیم در بحث مطرح شد، حتماً نحوه ارتباط آنها را برجسته کنید. همانطور که میدانیم میتوان از هر دو برای ایجاد گروههای مساوی استفاده کرد.
گام ششم؛ بازاندیشی
در پایان از دانشآموزان بپرسید:
- تقسیم چیست؟
دیدگاهتان را بنویسید