نوشتهی دیگری نوشتهام به نام «پنهان در فعالیتهای ریاضی» و در آن سوالهایی مطرح کردهام دربارهی آنچه غیر از دانش ریاضی، در فعالیتهای ریاضی پنهان شده است.
در این نوشته میخواهم دربارهی «ارزشهای ریاضی» بنویسم که چه خودآگاه و چه ناخودآگاه، پشت فعالیتهایی که برای کلاسهایمان طراحی یا انتخاب میکنیم، پنهاناند.
آلن بیشاپ۱ مقالهای دارد که در آن به ارزشها در ریاضی میپردازد. او ارزش یک شیء را بهطور کلی در سه دسته قرار میدهد که درک من از آنها این است:
- ارزشهایی که به پندارهی آن شیء مرتبط است (پنداره).
- ارزشهایی که به رابطهی فردی با آن مرتبط است (فردی).
- ارزشهایی که به رابطهی جامعه با آن مرتبط است (اجتماعی).
بیشاپ در هر کدام از این سه دسته، یک جفت ارزش ریاضی معرفی میکند که در جدول زیر آمده است:
پنداره (IDEOLOGY)
خردگرا (RATIONALISM)
واقعیتنما (OBJECTISM)
فردی (SENTIMENT)
کنترلکننده (CONTROL)
پیشرفتکننده (PROGRESS)
اجتماعی (SOCIOLOGY)
باز و در دسترس (OPENNESS)
رازگونه (MYSTERY)
در ادامه، درکم از تعریف بیشاپ از این سه جفت ارزش را مینویسم.
درک من از ارزشهای ریاضی بیشاپ
| پنداره- خردگرا اگر فقط بخواهیم یک ارزش برای ریاضی بیان کنیم، همین ارزش است! ریاضی خرد گرا است. در ریاضی میتوان ایده را از ابژه جدا کرد و روی ایدهها و ارتباط میان آنها به صورت منطقی کار کرد. این جدایی ایده از ابژه به ریاضیات فرصت میدهد که شکوفا شود و برای هر قدم به دنبال معنی بیرونی نگردد. این همان کاری است که ریاضیدانها انجام میدهند و میراث آن برای ما زیباییهایی است که درون ریاضی میبینیم؛ مثلاً یک اثبات زیبا بدون آنکه به مفهومی خارج از ریاضی متصل باشد. ریاضیآموزها باید از این ارزش ریاضی یعنی خردگرایی، انتزاع و نظریهپردازی ریاضی آگاه باشند. |
| پنداره- واقعیتنما ریاضی واقعیتنما است یعنی میتوان در ریاضی روی ایدههایی کار کرد که خاستگاه آنها ابژهها و مفاهیمی خارج ریاضی هستند و نه تنها ایدهها از تعامل ما با محیط سرچشمه میگیرند، بلکه این اشیاء مادی هستند که پایههای شهودی و تخیلی را برای این ایدهها فراهم میکنند. این ارزش به ریاضی معنی میبخشد و آموزش ریاضی باید این ارزش را نمایان کند. |
| فردی- کنترل کننده ریاضی میتواند سیستمهای طبیعی و اجتماعی را مدلسازی و پدیدهها و رفتارها را پیشبینی کند. کنترلکنندگی ریاضی آن را به ابزاری قدرتمند برای ایجاد کنترل محیطی و در نتیجه نوعی امنیت در جهان همیشه در حال تغییر تبدیل میکند. این یکی از ارزشهای ریاضی است که باید مورد توجه قرار بگیرد. |
| فردی- پیشرفتکننده ریاضی در حال پیشرفت است و گرچه اکنون میتواند برخی از سیستمها را مدلسازی و تحلیل کند ولی ناشناختههایی هست که ریاضی در پی شناخت آنها است. توجه به این ارزش در ریاضی میتواند شک، جستجو، کشف، دیدن جایگزینها و مهمتر از همه، ساختن دیدگاهها و باورهای جدید را ترغیب کند. |
| اجتماعی- باز و در دسترس حقایق، گزارهها و ایدههای ریاضی به طور کلی برای همه قابل بررسی است و هربار دوباره به آنها فکر کنی، میتوانی درستی آنها را نمایش دهی و اثبات کنی. از این جهت است که میتوان گفت ریاضی باز و مستقل از افراد است. مهمترین نتیجهی این ایده، این است که دانش ریاضی برای همه در دسترس است؛ کافیاست که رویهها را درست انجام دهید و قوانین را رعایت کنید، منطق، بقیهی کارها را انجام خواهد داد. یک معلم خوب باید به یادگیرنده کمک کند که این ارزش یعنی در دسترس بودن ریاضی را تجربه کند یعنی استدلال کند، نشان دهد یا توضیح دهد که چرا یک حقیقت ریاضی، چنین است. |
| اجتماعی- رازگونه گرچه ریاضی «باز و در دسترس» است، اما مردم هنوز در مورد اینکه ریاضیات چیست احساس ابهام میکنند و با وجود اینکه ریاضی، گستردهترین درس در سراسر جهان است، اما هنوز هم یکی از غیر شفافترین و رازگونهترین موضوعاتی است که اکثر یادگیرندگان نگران یادگیری آن هستند و نسبت به آن احساس نادانی میکنند. علاوه بر این، این فقط مردم معمولی نیستند که احساس میکنند ریاضیات یک راز است؛ ریاضیدانان نیز این احساس را دارند و در پی کشف رازهای آن هستند. اینها همان انسانهای ویژهای هستند که میتوانند با موجودات انتزاعی کار کنند و ایدههای نو بسازند. |
حالا به نوشتهی «پنهان در فعالیتهای ریاضی» بر میگردم و مثالهای آن نوشته برای ورود به اعداد مختلط را با این ارزشها بررسی میکنم.
اعداد مختلط و ارزشهای ریاضی
در نوشتهی «پنهان در فعالیتهای ریاضی» مثالهایی از شروعهای متفاوت اعداد مختلط آمده است. هر کدام از این شروعها، ارزشهایی را در خود دارد که معلم با طراحی یا انتخاب آنها در جهت پررنگ کردنشان تلاش کرده است.
پنداره- خردگرا
وقتی از اتصال درون ریاضی برای معرفی اعداد مختلط استفاده میکنیم، مثلا همانطور که در کتاب حساب دیفرانسیل و انتگرال۲ دیده میشود، نشان میدهیم که «رادیکال منفی یک» رفتار جبری مشابه اعداد دیگر از خود نشان میدهد:
![]()
یا وقتی با تعبیر هندسی آغاز میکنیم و از دوران ۱۸۰ درجه با ضرب یک عدد در «منفی یک» و دوران ۹۰ درجه با ضرب یک عدد در «رادیکال منفی یک» در صفحهی اعداد صحبت میکنیم:
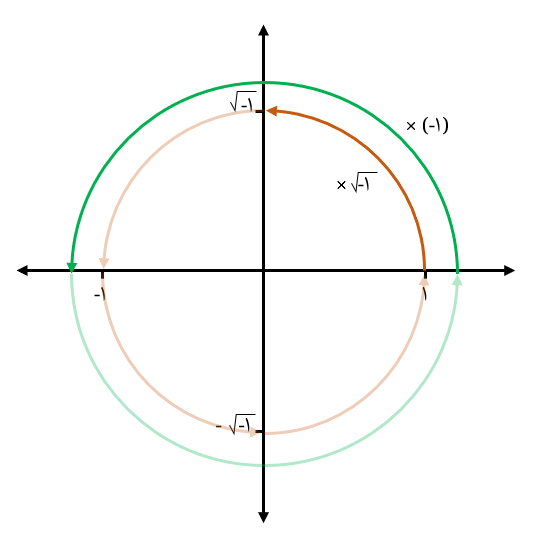
در جهت پررنگ کردن ارزش خردگرایی ریاضی حرکت میکنیم.
پنداره- واقعیتنما
«اعداد مختلط کاربردهای فراوانی دارند و برای مدل کردن پدیدهها در فیزیک پیشرفته بهکار میآیند.»
وقتی تأکید ما در گفتن جملهای مانند جملهی بالا روی ارتباط ریاضیات و واقعیت است، انگار درصدد هستیم که ارزش واقعیتنمایی ریاضی را نشان دهیم.
فردی- کنترل کننده
وقتی از کاربردهای اعداد مختلط در پیشبینی، کنترل و اصلاح اتفاقها صحبت میکنیم، وجه کنترلکنندگی ریاضی را مورد توجه قرار دادهایم.
فردی- پیشرفت
وقتی دربارهی این صحبت میکنیم که دو، سه قرن طول کشید تا مفهوم اعداد مختلط جای خود را در ریاضیات پیدا کنند و تعبیر معنایی دقیقی برای آنها ارائه شود. پیشرفت ریاضی را به عنوان یک ارزش مورد توجه قرار دادهایم.
اجتماعی- باز و در دسترس
وقتی اعداد مختلط را با فعالیتی که در آن یادگیرندگان فرصتی برای گفتن و شنیدن، ایدهپردازی، استدلال و ارزیابی ایدهها داشته باشند، آغاز میکنیم، برای نشان دادن در دسترس بودن ریاضی تلاش میکنیم. مثلاً این فعالیت:
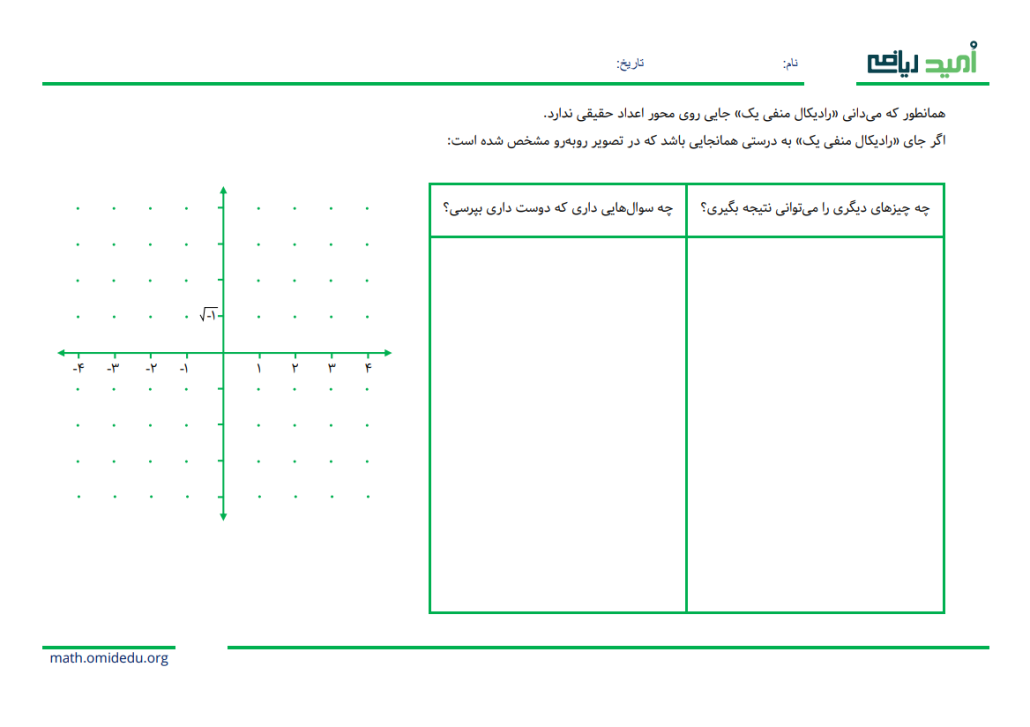
اجتماعی- رازگونه
وقتی از بزرگان ریاضی صحبت میکنیم که قرنها روی گسترش اعداد کار کرده و اعداد مختلط را به گونهای که ما اکنون با آنها برخورد میکنیم، صورتبندی کردهاند، رازگونگی ریاضی را به رخ میکشیم.
مستقل از آنکه این ارزشها به اندازه کافی با دقت بازشناسی شدهاند یا نه، ایدهی این نوشته این است که ما به عنوان معلم، چه بخواهیم یا نخواهیم، ارزشهای ریاضی را با خودمان و فعالیتهایمان به کلاس درس میبریم، خوب است روی این آنها تأمل کنیم و ببینیم که چه ارزشهای پنهانی را همراه با ایدههای ریاضی منتقل میکنیم. این بازاندیشی میتواند به ما کمک کند که سلیقهی خود را بهتر بشناسیم و ببینیم که توجهمان به کدام ارزشها بیشتر است و چرا.
ماجرا این است که آن ریاضیاتی که دانشآموزان به واسطهی فعالیتهای انتخابی ما تجربه میکنند، معنی ریاضی را برای آنها میسازد و نسبت خود با ریاضی را با همین معنی از ریاضی برقرار و تعیین میکنند و آگاهی ما از آنچه که از ارزشهای ریاضی در فعالیتهایمان پنهان است و توجه به آنها، میتواند انگارهای بهتر از ریاضی برای دانشآموزان بسازد.
پینوشت ۱.
گرچه بیشاپ، همهی این ارزشها را در کنار هم آورده است، اما این به معنی آن نیست که معلم باید به همهی ارزشها به طور یکسان بپردازد. پژوهشهای دیگری هست که نشان میدهد در مخاطبان هریک، برخی از ارزشها پررنگتر و برخی کمرنگتر است. در برخی از پژوهشها نیز روی برخی از ارزشها تأکید شده است و ایدهی آنها این است که شاید شرایطی که در آن قرار داریم و اهداف بزرگتری که دنبال میکنیم، ایجاب کند که برخی از ارزشها را بیشتر در برنامهدرسی ریاضی بیاوریم.
پینوشت ۲.
کار یکی از کارگروههای «امید ریاضی»، مطالعه و بررسی «استانداردهای آموزشی» و پژوهشهای مرتبط با آن است. «ارزشهای ریاضی» یکی از موضوعات مورد مطالعه در این کارگروه بوده است. از همهی دوستان این کارگروه بابت همفکریهایشان ممنونم. امیدوارم که این دوستان نیز دربارهی «ارزشهای ریاضی» از نگاه خودشان بنویسند.

دیدگاهتان را بنویسید