کتاب ریاضی سیاوش شهشهانی را ورق میزنم. در فصل سوم یعنی در آغاز معرفی اعداد مختلط، تاریخ شکلگیری این اعداد را هم دقیق و هم زیبا نوشته است. در همان صفحات اول این فصل، نام ریاضیدانهای زیادی آمده است که در کشف، صورتبندی و معرفی اعداد مختلط نقش داشتهاند. مثلاً این قسمت را ببینید:
«کاردانو در کتاب خود مقادیری مانند «رادیکال منفی یک» را «اعداد مجازی» قلمداد میکرد که هرچند خود عدد نیستند ولیکن رفتار جبری مشابه اعداد دارند و به کمک آنها میتوان به حقایقی دربارهی اعداد رسید، همچنان که پذیرفتن اعداد منفی در جبر، راه را برای بررسی اعداد مثبت هموارتر میکند.
طی دو تا سه قرن مفهوم «رادیکال منهای یک» و امثال آن جای خود را در ریاضیات یافت و تعبیر معنایی دقیقی برای آن ارائه شد. اولین افرادی که تعبیری هندسی برای آن ارائه دادند، مسّاح نروژی کاسپار وسل و حسابدار سوییسی ژان روبر آرگان بودند ولی بررسی جامع و دقیق اینگونه عدد و خواص جبری آنها در آثار ریاضیدان بزرگ آلمانی گاوس، به کمال رسید. روش برخورد امروزی با اعداد مختلط، روش گاوس است.»
سیاوش شهشهانی۱
هنگام خواندن این متن، سوالهای زیادی به ذهنم میآید:
- چه میشد اگر این مقدمه برای معرفی اعداد مختلط در کتاب نمیآمد؟
- این مقدمه چه پیامی برای خواننده دارد؟
- چه طورهای دیگری میتوان اعداد مختلط را آغاز کرد و پیامد هر کدام چیست؟
گشتی در وبگاههای مختلف میزنم و چند شروع دیگر را هم میبینم. در نمونههایی که به چشمم میخورد، اعداد مختلط یا بدون مقدمه شروع شده است یا در آغاز با دقتهای مختلف، تاریخ را مرور کرده است یا به کاربردهای اعداد مختلط ارجاع داده است یا با تعبیر هندسی آغاز شده است.
سوالهای من دربارهی این مقدمهها و همینطور دربارهی شروع بدون مقدمه، همچنان پابرجا است …
قبل از این که ادامه دهم، کمی به سلیقهی خودم برای آغاز اعداد مختلط نگاه میکنم. این یکی از فعالیتهایی است که احتمالاً در آغاز این درس به دانشآموزانم میدهم.
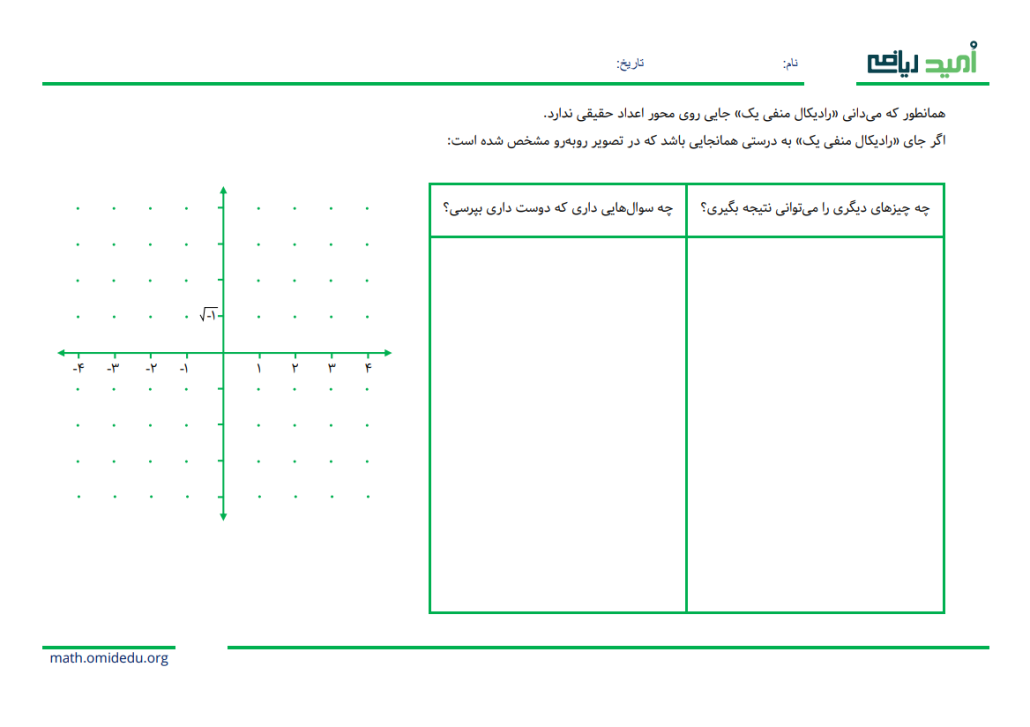
زمانی که مشغول مرتب کردن کاربرگ هستم، سوالهایی به سوالهای قبلیام اضافه میشود:
- معلم هنگام طراحی یا انتخاب فعالیتهای کلاسش به چه چیزهایی غیر از هدفهای ریاضی توجه میکند؟ آیا این توجه خودآگاه است یا ناخودآگاه؟
- سلیقهی معلم در طراحی یا انتخاب فعالیتها از کجا میآید؟
- آیا سلیقهی یک معلم در طراحی یا انتخاب فعالیتهایی که به کلاسش میبرد، همیشه یکسان است؟
به سوالهای بیشتری هم فکر میکنم:
- دانشآموزان در کلاسهای ریاضی، غیر از دانش ریاضی، چه چیزهای دیگری دربارهی ریاضی یاد میگیرند؟
- این دریافتها چه اثری بر نگاه آنها به ریاضی و ریاضیورزی میگذارد؟
و سوالهای دیگری که انگار تمامی ندارد …
این نوشته را همینجا تمام میکنم و در نوشتهی دیگری به نام «ارزشهای ریاضی» به آنها برمیگردم …
- شهشهانی، سیاوش. حساب دیفرانسیل و انتگرال-جلد اول. انتشارات فاطمی- ۱۳۹۴ ↩︎

دیدگاهتان را بنویسید