برای یادگیری احتمال، لازم است که شناختی از پدیدهی تصادفی ایجاد شود و گمان بنده این است که در برنامه درسی ما توجه کافی به شناخت کودک از پدیدهی تصادفی نشده است. پیشتر در نوشتهی «عاملیت، اراده و پدیدهی تصادفی» اشاره کردم که عدهای از بچهها در اولین مواجههها با پدیدهی تصادفی دنبال ارادهای میگردند که نتایج را کنترل کند. برنامه درسی باید به قول فیشبین، به کودک فرصت دهد که بتواند شهود جدیدش را از پدیدهی تصادفی بسازد.
در این نوشته تلاش میکنم وجه دیگری از شهود بچهها در مورد پدیدهی تصادفی را پیش بکشم و این بار هم در همین ابتدا بخشی از ایدهی را اینطور مینویسم: «عدهای از بچهها در مواجهه با پدیدههای تصادفی دنبالِ پیدا کردنِ صورتهایی از نظم هستند. این شهود از پدیدهی تصادفی باید به مرور و با برنامه در طول سالهای دبستان ترمیم شود.»
پیاژه و تیلههای رنگی۱
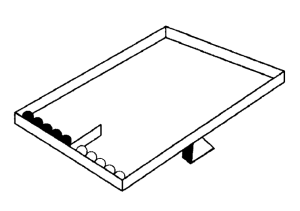
اگر موافقید نیم قرن عقب برویم و به پیاژه و اینهلدر و پژوهشهایشان سر بزنیم. آنها جعبهای مشابه تصویر را با تیلههای سفید و سیاهِ مرتب به بچهها دادند و از بچهها پرسیدند که اگر جعبه را تکان دهیم و دوباره همینطوری کج قرار دهیم که همهی تیلهها به سمتِ پایین برگردند، حدس میزنید تیلههای رنگی به چه ترتیبی قرار میگیرند. طبق نتایج، پاسخ بچههای کمتر از ۷ سال، شامل الگوهای منظم بود و عموم آنها باور داشتند که هر تیله سر جای خودش برمیگردد. در بین بچههای ۷ تا ۱۱ سال، هر چه سن بیشتر میشد، اشارات بیشتری به مخلوط شدنِ تیلهها در کلامشان دیده میشد و بچههای بزرگتر از ۱۱ سال بودند که مشخصاً به گوناگونیِ حالتهای مختلفی که ممکن است پیش بیاید اشاره میکردند.
گرین و دنبالهی سکهها۲
دیوید گرین در دههی نود در تحقیقش از ۳۰۰ دانشآموز خواست که دنبالهای پنجاهتایی از شیر و خط بنویسند و با این کار نتیجهی ۵۰ بار پرتاب سکه را شبیهسازی کنند. نتیجهی کار بچهها جالب است و اگر این نتیجه را با انتظار تئوری مقایسه کنیم (مثلاً تصور کنید که این سوال به ۳۰۰ کامپیوتر هم داده شود و نتایج آنها را با نتایج کار بچهها قیاس کنیم) جالبتر هم میشود.
| در هر برگه به طور میانگین ۲۴٫۵۶ بار «شیر» نوشته شده. | بسیار مطابق انتظار (۲۵) است. | |
| در ۷۰ درصد برگهها ۲۴ تا ۲۶ بار «شیر» نوشته شده است. | تقریباً دو برابرِ مقدار مورد انتظار است. | |
| ۱۸ نفر از ۳۰۰ نفر دقیقاً دنبالههای یکی در میان نوشتهاند (یعنی ۶٪ بچهها!). | احتمال این اتفاق، یک به روی ۵۰۰٬۰۰۰٬۰۰۰٬۰۰۰ است (یعنی ۰٫۰۰۰۰۰۰۰۰۰۲٪). |
باز هم شهود نوظهور
یک بار دیگر همین دو مورد پژوهش بالا را نگاه کنید. در آزمایش پیاژه کودکان کمسنتر پیشبینی میکردند که تیلهها با همان ترتیب اولیه در جای خود قرار میگیرند. در آزماش گرین، ۶٪ بچهها فکر میکردند که نتیجهی سکه کاملاً یکی در میان به دست میآید. همچنین در همین آزمایش عدهی غیر عادیای از بچهها تعداد شیر و خطها را (۲۵ و ۲۵) یا (۲۴ و ۲۶) یا (۲۶ و ۲۴) ثبت کردهاند. پژوهشهای دیگری هم میتوان پیدا کرد که در آنها تلاش کودک برای پیدا کردن سویههایی از نظم دیده میشود (مثلاً در پژوهشهای گرین ۱۹۷۹ ۳، تورسکی و کهنمن ۱۹۷۲ ۴و چیسی و پریمی ۲۰۰۹ ۵).
به کلاسهایمان برگردیم. غیر از این است که ما دائماً در ریاضی و شاید حتی حوزههای دیگر از بچهها میخواهیم که الگوهای منظم ببینند و به اتکای این الگوها، ناشناختهها را پیشبینی کنند؟ پرداختن به پدیدهی تصادفی همان جاییست که این قاعده قدری به هم میریزد. حالا از منظری دیگر شاید روشن شده باشد که چرا فیشبین میگوید: «احتمال به شیوهای از فکر نیاز دارد که واقعاً با بیشتر آنچه در ریاضیات مدرسه آموزش داده میشود، متفاوت است. برای یاد گرفتنِ احتمال، دانشآموز باید شهود جدیدی برای خود بسازد۶.»
اگر در فرآیند کلاس ریاضی، فرصتهایی ویژه برای مشاهدهی دنبالههای تصادفی دیده نشده باشد، اگر بچهها فرصت کافی برای فاصله گرفتن از شهود الگومحور خود و ساختن شهود جدید را نداشته باشند و درکی از بینظمیِ ترتیبیِ دنبالهی تصادفی نداشته باشند، با کودکان روبهرو میشویم که:
- انتظار دارند سکه یکی در میان پشت و رو بیاید (مثل مشاهدهی گرین ۱۹۹۱)
- اگر از کیسهی تیلههای آبی و سبز (۱۵ تا و ۱۵ تا)، ۴ بار پشت سر هم آبی بیرون بیاید، احتمال سبز یا آبی آمدنِ تیلهی بعدی را همشانس نمیدانند (مثل مشاهدهی چیسی و پیمی ۲۰۰۹)
- بین دو دنبالهی «شششخخخ» و «شخخششخ» (ش به معنای شیر و خ به معنای خط)، برایشان قدری عجیب میآید که اولی تصادفی تولید شده باشد (مثل مشاهدهی تورسکی و کهنمن ۱۹۷۲)
- و هزار و یک مشاهدهی دیگری که هر کدام از ما سر کلاسهایمان دیدهایم.
میخواهم ورق زدن کتابهای درسی را به عهدهی خوانندهی این نوشته بگذارم. امیدوارم بگردید و ببینید در تمام طول دبستان، از بین (اگر اشتباه نکنم) ۱۴ تمرینی که از کودک خواسته شده آزمایشی تصادفی انجام دهد و نتایج را ثبت کند، چند بار این فرصت به او و کلاس درس داده شده که در مورد دنبالهی نتایجشان فکر و گفتگو کنند. بیشتر از این نمیخواهم در مورد کتاب چیزی بگویم چون قصدم این است که همین ۱۴ مثال کتاب را در نوشتهای دیگر از زوایای دیگری بررسی کنم.
- Piaget, J. and Inhelder, B. (1975) The Origin of the Idea of Chance in Children. London: Routledge and Kegan Paul. ↩︎
- Green, D. R. (1991). A longitudinal study of pupils’ probability concepts. In D. Vere-Jones (Ed.), Proceedings of the Third International Conference on Teaching Statistics (Vol. 1, pp. 320-328). Voorburg, The Netherlands: International Statistical Institute. ↩︎
- Green, D.R. (1979) The chance and probability project. Teaching Statistics, 1(3), 66–۷۱. ↩︎
- Kahneman, D. and Tversky, A. (1972) Subjective probability: A judgment of representativeness. Cognitive Psychology, 5, 207–۲۳۲. ↩︎
- Chiesi, F., & Primi, C. (2009). Recency Effects in Primary-Age Children and College Students. International Electronic Journal of Mathematics Education, 4(3), 259-279. ↩︎
- Fischbein, E., & Schnarch, D. (1997). The evolution with age of probabilistic, intuitively based misconceptions. Journal of Research in Science Teaching, 28, 96-105. ↩︎

دیدگاهتان را بنویسید