در این نوشته تلاش میکنم نشان دهم بچهها حق دارند معنیِ ضرب کسرها را نفهمند!
اما قبل از شروع نوشته، لازم است صورت مسئله را روشن کنم.
گر چه دانشآموزان زیادی در محاسبهی ضرب کسرها مشکل دارند اما این نوشته میخواهد در مورد چیز دیگری صحبت کند.
گر چه دانشآموزان زیادی در درک و حلِ مسئلهی کلامی (به خصوص وقتی پای کسر در میان باشد) مشکل دارند اما مجدداً باید عرض کنم که این نوشته میخواهد در مورد چیز دیگری صحبت کند.
پس این نوشته میخواهد در مورد چه چیزی صحبت کند؟ در خطوط زیر دانشآموزی را تصویر میکنم که معمولاً برای معلم کلاس پنجم آشناست:
دانشآموز الف، وقتی با صورت مسئلهای مثلِ «۴ عدد نان داریم. دو سوم از نانها مصرف شده است. میخواهیم مقدار نان مصرف شده را حساب کنیم.» روبهرو میشود، دست به کار میشود، شاید شکل بکشد و به کمک درکش از کسر، پاسخ صحیح را پیدا میکند.
همین دانشآموزِ الف، در مواجهه با سوالِ \(\frac ۲ ۳ × ۴\) میتواند از آموختههای فنیِ خود در مورد ضرب کسرها استفاده کند و پاسخ را پیدا کند (مثلاً ممکن است او یاد گرفته باشد که باید ۴ را در صورت کسر ضرب کند و پاسخ را بیابد).
اما متاسفانه دانشآموز الف، ارتباط بین مسئلهی کلامی (که میفهمد) و ضرب کسرها (که بلد است) را درک نمیکند.
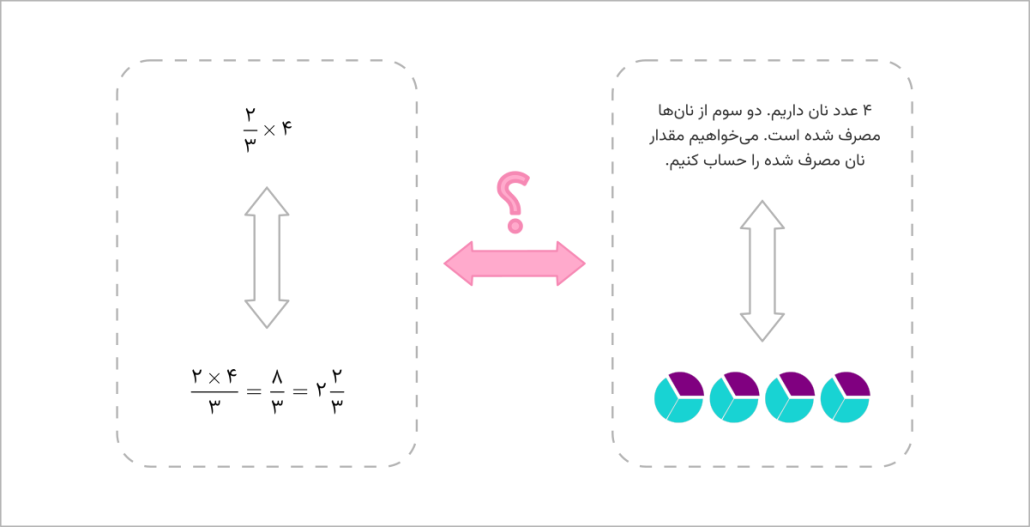
اگر بخواهم در چارچوب تصویر بالا صحبت کنم، در واقع دانشآموز الف با کمک درک خود از کسر، ارتباطی را که در خطچین راست وجود دارد میفهمد. همچنین او ارتباطی را که در خطچین چپ وجود دارد به لحاظ فنی بلد است. اما ارتباط صورتیرنگ برای او ناشناخته است.
شاخصترین جایی که مشکلِ دانشآموز الف بروز پیدا میکند، زمانیست که او مسئله را میخواند و میتواند به آن فکر کند و شاید با شهودش یا به کمک رسم شکل به پاسخ هم برسد اما وقتی از او میخواهی که مسئله را به صورت عبارت ریاضی بنویسد، هاج و واج نگاه میکند و نمیداند که این همان «ضربِ کسرها» است. در واقع «ضرب کسرها» به «معنا» وصل نشده است.
قصدِ این نوشته این است که بگوید «دانشآموز الف، حق دارد». کتاب درسی به ارتباط صورتیرنگ توجه نکرده است.
مشکل از کجاست؟
شاید این مشکل را هم بگذارید کنار دشواریهای یادگیریِ کسر. اما از قضا این بار مشکل از کسرِ بینوا نیست. این بار گویا مشکل از ضرب است. ضربی که ما از کلاس سوم به دانشآموزان آموختهایم، یک ویژگی خاص داشته است. پیش از این، عملوند اولِ همهی ضربهای ما، «تعدادی» از چیزی را نشان داده است. نگاه کنید:
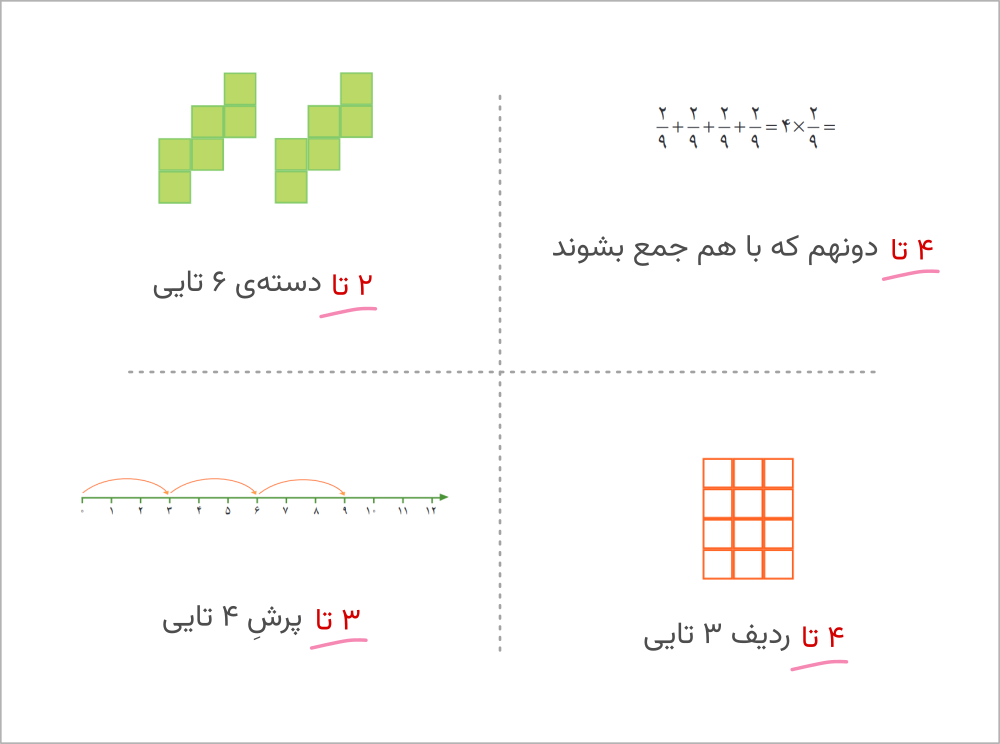
اما حالا وقتی به ضرب کسر در عدد طبیعی و ضرب کسر در کسر میرسیم، عملوند اول، کسر است و نمیتواند بیانگرِ «تعدادی» از چیزی باشد. به همین دلیل است که دانشآموز نمیتواند ضرب را در موقعیت جدید، به معنایی که از قبل میشناخته ربط دهد.
| \[۳ × ۴\] | ۳ تا ۴ |
| \[ ۳ × \frac ۱ ۴ \] | ۳ تا یکچهارم |
| \[\frac ۱ ۳ × ۴\] | یکسوم تا ۴ (!) |
| \[\frac ۱ ۳ × \frac ۱ ۴\] | یکسوم تا یکچهارم (!) |
توجه کنید که مقصود از حرفهای بالا فقط این نیست که وقتی به ضربِ کسر میرسیم، نیاز به تغییر در جملهبندی زبانِ فارسی خواهیم داشت و مشکل از همین ویژگیِ زبانی ناشی میشود! تفاوتی که با ورود ضرب به حوزهی اعداد کسری ایجاد میشود، چیزی بیش از جنبهی زبانیِ آن است. همانطور که قبلتر اشاره شد، نکتهی اصلی اینجاست که ضرب در سالهای سوم و چهارم، به گونهای معرفی شده است که عملوند اولِ آن بیانگرِ «تعداد» بوده است و حالا با ورود به کسر، این معنای ضرب جوابگو نیست.
چشمهای بستهی کتاب درسی
ضرب کسر در عدد طبیعی و ضرب کسر در کسر، در کلاس پنجم و در صفحههای ۳۳ و ۳۴ معرفی شده است. هر کدام از این موارد، طی یک «فعالیت» پیش کشیده شده و کتاب برای حل مسئله از ضرب استفاده کرده است. اما هیچ اشارهای نکرده که چرا برای این مسئلهها میتوانیم از «ضرب» استفاده کنیم.
همانطور که در بندهای بالا گفته شد، معنایی که دانشآموز در سالهای پیش، از ضرب میشناخت، با معنایی که اینجا به کار میآید، متفاوت است. معنای جدید ضرب، باید به درستی و از سرِ صبر در ذهن دانشآموز شکل بگیرد تا بتواند درک کند که چرا این موقعیت را هم میتوان به صورتِ ضرب نوشت. اما کتاب درسی گویا چشمش را روی این موضوع بسته و فهمیدن را به کودک واگذار کرده است. نتیجهی این برخورد کتاب درسی، چیزی جز این نیست که با دانشآموزانی (مثل دانشآموز الف) مواجهیم که در ذهنشان ضرب کسرها به معنایی وصل نشده است.
به عنوان معلم چه کار کنیم؟
حداقلیترین کار که به عنوان معلم میتوانیم انجام دهیم، این است که به این کاستی کتاب درسی آگاه باشیم و مشکل دانشآموزان را بفهمیم. اما اگر قدم بهتری میخواهیم برداریم، بهتر است از قبل به فکر این باشیم که بچهها با معناهای دیگری از ضرب هم آشنا شوند. بله! ضرب میتواند به شیوههای مختلف معرفی شود. به مرور در همین وبگاه، شیوههای متنوعی برای معرفی ضرب معرفی خواهد شد. فعلاً در حد اشاره، یکی از این شیوهها را که به طور مهجوری در (فقط) یکی از تمرینهای کتاب عنوان شده، پیش میکشم۱:
در صفحههای ۶۶ کتاب سال سوم، تمرینی وجود دارد که ضرب را به عنوان «چند برابری» معرفی کرده است۲.

به وقتش در مورد ضرب با تعبیرِ «چند برابری» خواهیم نوشت. فعلاً شاید در همین حد کافی باشد که در این تعبیرِ ضرب، میتوان به ضرب عددهای کسری هم راحتتر فکر کرد. مثلاً اگر دانشآموز به قدر کافی با ضرب به معنای «چند برابری» کار کرده باشد، به راحتی میتواند به ۲٫۵ برابرِ تعداد سیبها هم فکر کند. نه؟
- دوست گرانمایهای بعد از مطالعهی متن پیشنهاد کرد تاکید کنم که قرار نیست این نوشته تعبیر «چند برابری» ضرب را به عنوان یگانه راهحلِ چالش مطرح شده، معرفی کند. واقعاً میشود ضرب را به شکلهای محتلفی معرفی کرد و بعضی از آنها برای پاسخ دادن به چالش فوق کارا هستند. تعبیر «چند برابری» فقط به عنوان مثال در این متن عنوان شد. ↩︎
- پس از نگارش این متن، دوست عزیزی (نامساوی با دوستِ گرانمایهی پانوشت قبل) یادآوری کرد که در صفحهی ۶۶ آخرین ویرایش کتاب هم اشارهای به ضرب به عنوان چند برابری شده است. اشارهی کتاب کماکان ناچیز است اما لازم بود که در اینجا قید شود. ↩︎

دیدگاهتان را بنویسید