این اولین نوشته از مجموعهای نوشته خواهد بود که هدف آنها به نمایش گذاشتن گنجهای پنهان در جدول ضرب است. در خود این نوشتهها در مورد چگونگی استفاده از آنها در کلاس درس توصیهای نمی شود. ولی امیدوارم هر کدام از آنها شروعی باشد برای تولید فعالیتهایی که در تارنمای امید ریاضی خواهند آمد.
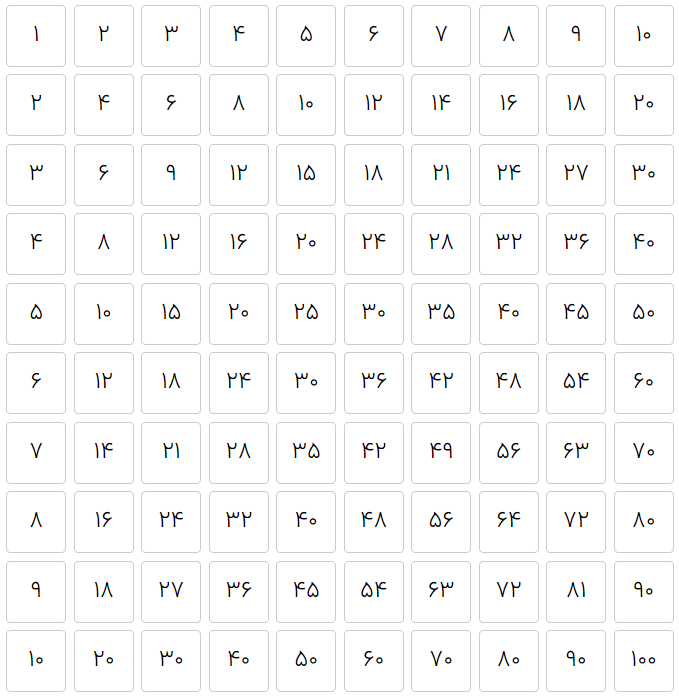
با یکی از شگفتانگیزترین مشاهدات جدول ضربی شروع میکنم. برای راحتی به جای استفاده از «جدول ضرب ده در ده» از «جدول ضرب پنج در پنج» استفاده میکنم.

خانههای جدول را ردیف به ردیف جمع میزنیم و با کمک آن مجموع اعداد را پیدا میکنیم.
(تفاوت رنگ در شکل زیر هیچ خاصیتی ندارد، به جز اینکه توجه را به ردیفها جلب میکند).

ردیف اول
\[(۱+۲+۳+۴+۵)\]
هشدار. به هوش باش. به گوش بیاویز. با جان بشنو.
«اگر دنبال ساختار هستید، تا زمانی که واقعا لازم است، محاسبه نکنید.» رعایت همین دستور شاید سال ها برای یادگیرندهها طول بکشد. بنابراین تا میتوانید موقعیت برای تجربهی آن ایجاد کنید.
ردیف دوم
\[۲+۴+۶+۸+۱۰=۲(۱+۲+۳+۴+۵)\]
ردیف سوم
\[۳+۶+۹+۱۲+۱۵=۳(۱+۲+۳+۴+۵)\]
ردیف چهارم
\[۴+۸+۱۲+۱۶+۲۰=۴(۱+۲+۳+۴+۵)\]
ردیف پنجم
\[۵+۱۰+۱۵+۲۰+۲۵=۵(۱+۲+۳+۴+۵)\]
حالا همه سطرها را با هم جمع میکنیم و با فاکتورگیری از سطر اول (به معنای ریاضیِ فاکتورگیری) خواهیم داشت:
مجموع همهی اعداد جدول \((۱+۲+۳+۴+۵)(۱+۲+۳+۴+۵)=\)
حالا مجموع همه اعداد را با استفاده از ساختار زیر دوباره پیدا میکنیم.

قطعه اول
\[۱\]
قطعه دوم
\[۲+۴+۲=۲^۳\]
قطعه سوم
\[۳+۶+۹+۶+۳=۳^۳\]
قطعه چهارم
\[۴+۸+۱۲+۱۶+۱۲+۸+۴=۴^۳\]
قطعه پنجم
\[۵+۱۰+۱۵+۲۰+۲۵+۲۰+۱۵+۱۰+۵=۵^۳\]
حالا همهی قطعهها را با هم جمع میکنیم:
مجموع همهی اعداد جدول \(۱^۳+۲^۳+۳^۳+۴^۳+۵^۳=\)
حالا حرف آن ریاضیدان که میگفت «ریاضیات چیزی نیست جز بیان چیزهای یکسان به روشهای مختلف» اینجا به کار میآید.
ما دو ساختار مختلف به کار بردیم که هر دو، یک مجموع را برای ما حساب کردند؛ پس آنچه بدست آمده، باید با هم برابر باشند:
\[۱^۳+۲^۳+۳^۳+۴^۳+۵^۳=(۱+۲+۳+۴+۵)^۲\]
یعنی خداییش «اگر این جادوگری نیست، پس چی است!»

دیدگاهتان را بنویسید