در چند سال اخیر به کررات با تجربههایی در کلاس چهارم مواجه شدهام که معلم در آموزش تقسیم با مشکلاتی روبهرو بوده است. شکل مواجههی کتاب درسی با تقسیم در کلاس چهارم، نسبت به آنچه در زمانِ ما آموزش داده میشد، تغییر کرده و البته به پررنگی روشن است که ایدهی این تغییر تلاش داشته که تقسیم را از یک فرایند صرفاً رویهای به تجربهای مفهومی تبدیل کند؛ از این بابت، به نظر بنده کتاب گامی به جلو برداشته است. آنچه در ذهن دارم که حاصل گفتگوها و تلاشهای من و فائزه شیخعلیان و آیدا حلالزاده بوده، احتمالاً در یک نوشته نمیگنجد و در آیندهی نزدیک تلاش میکنم آن را کامل کنم؛ اما در این نوشته قصد دارم به رابطهی گستردهنویسی عدد و تقسیم بپردازم.
اولین شعبدهی گستردهنویسی در حسابِ ابتدایی زمانی دیده میشود که کودک میخواهد عددهای چند رقمی را با هم جمع کند. مثلاً فرض کنید کودک میخواهد ۲۶ را با ۲۵ جمع کند. کافیست گستردهی این دو عدد را در پایهی ۱۰ به خاطر بیاورد. اجیمجیلاترجی… جمع ۲۶ و ۲۵ به جمع اعداد یک رقمی فروکاسته شد. چرا که حالا میتواند ۶ و ۵ را با هم جمع کند و ۲ تا دهتایی و ۲ تا دهتایی را با هم که هر دو هم آسان است و تمام. همین داستان در تفریق هم برقرار است.
هنگامی که کودک به ضرب چند رقمی میرسد هم شعبدهی گسترده دیدنِ اعداد در پایهی ۱۰، کار میکند. فرض کنید میخواهد ۳ را در ۲۳ ضرب کند. باز هم کافیست ۲۳ را به صورت ۲ تا دهتایی و ۳ تا یکی تبدیل کند و اجیمجیلاترجی… باز هم ضربمان به ضرب اعداد یک رقمی فروکاسته شد.
پس احتمالاً شعبدهی گستردهنویسی در پایهی ۱۰، در تقسیم هم کار را راه میاندازد!
به نظر میرسد کتاب درسی هم همین روند را در پیش گرفته است.
تقسیم در کتاب درسی
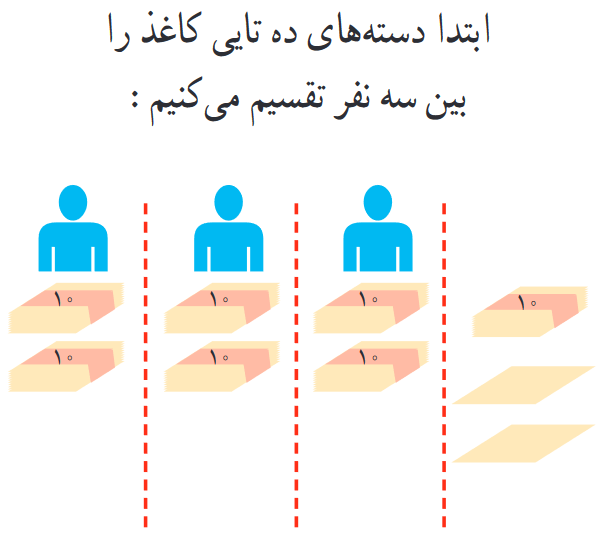
در صفحهی ۶۵ کتاب سال چهارم، قرار است ۷۲ برگه کاغذ بین ۳ نفر تقسیم شود. بنابراین کتاب، ۷۲ را به صورت ۷ دستهی دهتایی و ۲ تا یکی دیده و اجیمجیلاترجی… عالی شد نه؟ ۷ دستهی دهتایی را بین ۳ نفر قسمت میکنیم که به هر نفر ۲ دستهی دهتایی میرسد. در ادامهی کار، یک دستهی دهتایی و ۲ تا یکی داریم که باید بین ۳ نفر تقسیم شود. در این مرحله با عینکِ یکیای به عددمان نگاه میکنیم که میشود ۱۲ تا یکی و این ۱۲ تا هم که مثلِ آبِ خوردن بین ۳ نفر تقسیم میشود. در نهایت به هر نفر ۲۴ تا برگه میرسد و شعبدهی گسترده دیدنِ ۷۲ به صورت دستههای دهتایی و یکی جواب داد.
چند صفحه جلوتر کودک با تقسیمهای چند رقم بر چند رقم مواجه میشود. کتاب پیشنهاد میکند که کودک با تقریب زدنِ عددها کار را ساده کند. مثلاً برای تقسیم ۶۷۵ بر ۲۱، پیشنهاد میکند که ابتدا عددها را تقریب بزند و ۶۰۰ تقسیم بر ۲۰ را حساب کند که آسان است و بعد…
عالی شد نه؟
روش پیشنهادی کتاب را خلاصه میکنم:
مقسوم را به صورت گسترده بنویس و تقسیم کن و تمام؛ اما اگر کار دشوار بود، اول تقریب بزن و بعد برو سراغ گستردهنویسی.
روش کتاب همیشه جواب میدهد؟
بگذارید عددها را کمی عوض کنیم و امتحان کنیم. مثلاً بیایید ۴۰۰ را بر ۶۰ تقسیم کنیم:
تقریب که معنی ندارد. پس لابد باز هم شعبدهی گستردهنویسی راهگشاست.
- بیایید ۴۰۰ را به صورت ۴ دستهی صدتایی ببینیم. باید ۴ دستهی صدتایی را بین ۶۰ نفر تقسیم کنیم؛ خب! متاسفانه نمیتوانیم ۴ تا چیز را بین ۶۰ نفر قسمت کنیم.
- پس با عینکِ دستههای دهتایی ببینیم. باید ۴۰ دستهی ۱۰ تایی را بین ۶۰ نفر تقسیم کنیم؛ خب! باز هم نمیشود ۴۰ تا چیز را بین ۶۰ نفر تقسیم کنیم.
- پس با عینک یکیایها ببینیم. ۴۰۰ تا یکی را بین ۶۰ نفر تقسیم کنیم. بله! این شدنیست… اما چهطوری؟ انگار از ابتدا دنبال همین بودیم. نه؟ برگشتیم خانهی اول!
کفگیر شعبدهی گستردهنویسی به ته دیگ خورد!
حتماً متوجه هستید که موضوع فقط همین یک مثالی که ارائه کردم نیست. شما هم میتوانید صدها مثال دیگر بنویسید که روش کتاب در مورد آنها کاری از پیش نمیبرد. توجه کنید که من از اعداد بزرگی استفاده نکردم و ضمناً هر دو رُند بودند. اگر میخواهید بیشتر به مشکلات کار پی ببرید، پیشنهاد میکنم عددها را اندکی بزرگتر در نظر بگیرید. مثلاً خودتان را جای کودک بگذارید و با شیوهی کتاب، ۴۰۰۰ را تقسیم بر ۶۰ کنید (گمان میکنم بیجا نباشد که انتظار داشته باشیم بچهها از پس این تقسیم بربیایند).
یک گام به جلو؛ اما ناقص
میخواهم جملهای را که در ابتدا گفتم، دوباره تکرار کنم. در قیاس با آنچه در زمان ما آموزش داده میشد، مؤلفین به نیکی تلاش کردهاند که تقسیم را از یک فرآیندِ صرفاً رویهای به تجربهای مفهومی تبدیل کنند و بیشک من هم این را گامی به جلو میبینم اما گویا شیوهای که ارائه شده، نواقصی دارد. نتیجهی این نواقص، بنا بر مشاهدههای من (که البته چندان زیاد نیست) این است که معلم چهارم دبستان ناچار است دوباره سراغ شیوهی رویهای سابق برود و اگر او هم این کار را نکند، معلم کلاس ششم (کلاس پنجم بازگشتی به تقسیم ندارد) حتماً این کار را میکند.
مسأله، چگونه شکستن است
اگر اندکی از دورتر نگاه کنیم، ایدهای پشت پیشنهادِ گستردهنویسی هست که در عین سادگی، راهگشاست. در واقع ایدهی اصلی این است که «اگر میخواهی فلان محاسبه را انجام دهی و برایت دشوار است، عددها را به قسمتهای کوچکتری بشکن که کار سهل شود». مثلاً اگر میخواهی ۲۵ و ۲۶ را با هم جمع کنی، بهتر است آنها را به عددهای کوچکتری بشکنی که کار راحت شود. یا اگر میخواهی ۳ را در ۲۳ ضرب کنی، بهتر است ۲۳ را به عددهای کوچکتری بشکنی و بعد ادامه بدهی.
تبدیل کردنِ عددِ بزرگ به عددهای کوچک، ایدهی درخشانیست که ضرب و جمع و تفریق را آسان میکند. همچنین، همین روش میتواند تقسیم را هم ساده کند اما بگذارید یک لحظه به این سوال فکر کنیم که آیا شکستنِ عددها، حتماً باید به دستههای دهتایی و صدتایی و… باشد؟
در مثال بالاتر، طبق پیشنهاد کتاب، تلاش کردیم که برای تقسیم ۴۰۰ بر ۶۰، ۴۰۰ را به دستههای صدتایی یا دهتایی بشکنیم و متاسفانه دیدیم که هیچ کمکی به ما نکرد. حالا یک لحظه با ذهن آزاد به سوال فکر کنید. اگر شما در زندگی روزمره بخواهید ۴۰۰ را بر ۶۰ تقسیم کنید، چه میکنید؟ حتماً پاسخها گوناگون است. من یکی از پاسخها را میگویم: خیلی از ما ۴۰۰ را در ذهنمان میشکنیم اما به ۳۶۰ و ۴۰!
بله. انگار در تقسیمها، گاهی شکل دیگری از شکستن به کار میآید. یادمان باشد که عددها را بر حسب نیازمان میتوانیم به شکلهای مختلف بشکنیم. یکی از این شیوههای مختلفِ شکستنِ عددها این است که به دستههای دهتایی و صدتایی و … بشکنیم که به این کار گستردهنویسی در پایهی ۱۰ میگوییم. گستردهنویسی فقط یکی از شیوههای مختلف شکستن عددهاست. دوست دارم اشاره کنم که حتی در موقعیتهای جمع و تفریق و ضرب هم ضرورتی ندارد که ما حتماً عددها را بر پایهی ۱۰ بشکنیم (اگر مایلید به جمعی که در ابتدای همین نوشته ارائه شد برگردید و ببینید که بسیاری اوقات خود شما هم این جمع را در ذهنتان به صورت ۲۵ و ۲۵ و ۱ محاسبه میکنید).
میخواهم اینطور جمعبندی کنم: برای تقسیم هم مانند جمع و تفریق و ضرب، باید عددهایمان را به عددهای کوچکتری بشکنیم که کار راحت شود. اما تفاوتی بین تقسیم با بقیه وجود دارد. وقتی با جمع و منها و ضرب روبهرو هستیم، شکل خاصی از شکستنِ اعداد یعنی گستردهنویسی در پایهی ۱۰، همیشه راهگشاست اما وقتی با تقسیم روبهرو هستیم، بسیاری اوقات باید عددها را جور دیگری خرد کرد. در نوشتهی دیگری به این موضوع خواهم پرداخت.

دیدگاهتان را بنویسید